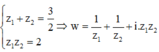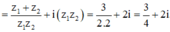Các câu hỏi tương tự
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
+
z
)
z
¯
. A. -2 B. 0. C. -...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho hai số phức z,w thoả mãn |z-1-i|=1,| w ¯ -2-3i|=2. Giá trị nhỏ nhất của |z-w| bằng
A. 13 -3.
B. 17 -3.
C. 17 +3.
D. 13 +3
Cho hai số phức z, w thỏa mãn
z
−
3
−
2
i
≤
1
w
+
1
+...
Đọc tiếp
Cho hai số phức z, w thỏa mãn z − 3 − 2 i ≤ 1 w + 1 + 2 i ≤ w − 2 − i .
Tìm giá trị nhỏ nhất P min của biểu thức P = z − w .
A. P min = 3 2 − 2 2
B. P min = 2 + 1
C. P min = 5 2 − 2 2
D. P min = 2 2 + 1 2
Cho hai số phức z,w thỏa mãn
z
−
3
−
2
i
≤
1
w
+
1
+...
Đọc tiếp
Cho hai số phức z,w thỏa mãn z − 3 − 2 i ≤ 1 w + 1 + 2 i ≤ w − 2 − i . Tìm giá trị nhỏ nhất P m i n của biểu thức P = z − w .
A. P min = 3 2 − 2 2
B. P min = 3 2 + 2 2
C. P min = 2 + 1
D. P min = 5 2 − 2 2
Cho các số phức z thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
(
2
-
i
)
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A.
x
-
7
y
-
9
0...
Đọc tiếp
Cho các số phức z thỏa mãn z - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = ( 2 - i ) z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x - 7 y - 9 = 0
B. x + 7 y - 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Cho số phức z thỏa mãn
z
−
1
−
i
1
, số phức w thỏa mãn
w
¯
−
2
−
3
i
2
. Tìm giá trị nhỏ nhất của
z
−
w
....
Đọc tiếp
Cho số phức z thỏa mãn z − 1 − i = 1 , số phức w thỏa mãn w ¯ − 2 − 3 i = 2 . Tìm giá trị nhỏ nhất của z − w .
A. 17 + 3
B. 13 + 3
C. 13 - 3
D. 17 - 3
Cho số phức z thỏa mãn
z
-
1
-
i
1
, số phức w thỏa mãn
w
¯
-
2
-
3
i
2
. Tính giá trị nhỏ nhất của
z
-
w...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Cho hai số phức z, w thỏa mãn
m
a
x
z
;
z
-
1
-
i...
Đọc tiếp
Cho hai số phức z, w thỏa mãn m a x z ; z - 1 - i ≤ 1 w + 1 + 2 i ≤ w - 2 - i . Tìm giá trị nhỏ nhất của biểu thức P = z - w
A. 2 - 1
B. 0
C. 1 6
D. 2 2 - 1
Số nghiệm phức của phương trình
z
+
2
|
z
|
+
3
-
i
(
4
+
i
)
|
z
|...
Đọc tiếp
Số nghiệm phức của phương trình z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
A. 1.
B. 2.
C. 3.
D. 4.
Cho số phức z thay đổi hoàn toàn thỏa mãn:
z
−
i
z
−
1
+
2
i
. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn:
w
2
−...
Đọc tiếp
Cho số phức z thay đổi hoàn toàn thỏa mãn: z − i = z − 1 + 2 i . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = 2 − i z + 1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. − x + 7 y + 9 = 0.
B. x + 7 y − 9 = 0.
C. x + 7 y + 9 = 0.
D. x − 7 y + 9 = 0.