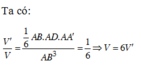Các câu hỏi tương tự
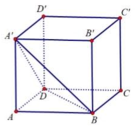
Gọi V là thể tích của hình lập phương ABCD.A’B’C’D’,
V
1
là thể tích tứ diện A’ABD. Hệ thức nào sau đây đúng? A.
V
3
V
1
B.
V
4
V
1
C.
V
6
V
1
D.
V
2
V...
Đọc tiếp
Gọi V là thể tích của hình lập phương ABCD.A’B’C’D’, V 1 là thể tích tứ diện A’ABD. Hệ thức nào sau đây đúng?
A. V = 3 V 1
B. V = 4 V 1
C. V = 6 V 1
D. V = 2 V 1
Gọi V là thể tích hình lập phương ABCD.A’B’C’D’,
V
1
là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng A. V 6
V
1
B. V 4
V
1
C. V 3
V
1
D. V 2
V
1
Đọc tiếp
Gọi V là thể tích hình lập phương ABCD.A’B’C’D’, V 1 là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng
A. V= 6 V 1
B. V= 4 V 1
C. V= 3 V 1
D. V= 2 V 1
Tính thể tích V của khối lập phương ABCD.A B C D , biết ACa
3
A. V 3
3
a
3
B. V 27
a
3
C. V
a
3
D. V 3
a
3
Đọc tiếp
Tính thể tích V của khối lập phương ABCD.A' B' C' D' , biết AC'=a 3
A. V= 3 3 a 3
B. V= 27 a 3
C. V= a 3
D. V= 3 a 3
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V A.
11
2
a
3
216
B.
7...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V. A.
11
2
a
3
216
B.
7
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có
A
B
a
,
A
A
2
a
.
Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′. A.
4
a
3
B. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
Cho khối tứ diện OABC có OA, OB, OC đôi một vuông góc và OA a, OB b, OC c. Thể tích V của khối tứ diện OABC được tính bởi công thức nào sau đây? A.
V
1
6
a
.
b
.
c
B.
V...
Đọc tiếp
Cho khối tứ diện OABC có OA, OB, OC đôi một vuông góc và OA = a, OB = b, OC = c. Thể tích V của khối tứ diện OABC được tính bởi công thức nào sau đây?
A. V = 1 6 a . b . c
B. V = 1 3 a . b . c
C. V = 1 2 a . b . c
D. V = 3 a . b . c
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức: A.
V
a
b
c
B.
V
1
3
a
b
c
C.
V
1
2
a
b
c
D.
V
3
a
b
c
Đọc tiếp
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
A. V = a b c
B. V = 1 3 a b c
C. V = 1 2 a b c
D. V = 3 a b c
Khối đa diện nào dưới đây có công thức tính thể tích là
V
1
3
B
h
(với B là diện tích đáy; h là chiều cao) A. Khối chóp B. Khối lăng trụ C. Khối lập phương D. Khối hộp chữ nhật
Đọc tiếp
Khối đa diện nào dưới đây có công thức tính thể tích là V = 1 3 B h (với B là diện tích đáy; h là chiều cao)
A. Khối chóp
B. Khối lăng trụ
C. Khối lập phương
D. Khối hộp chữ nhật