Phương trình cos 2 x − π 3 − m = 2 ⇔ cos 2 x − π 3 = m + 2.
Phương trình có nghiệm ⇔ − 1 ≤ m + 2 ≤ 1 ⇔ − 3 ≤ m ≤ − 1
→ m ∈ ℤ S = − 3 ; − 2 ; − 1 ⇒ T = − 3 + − 2 + − 1 = − 6.
Chọn đáp án B.
Phương trình cos 2 x − π 3 − m = 2 ⇔ cos 2 x − π 3 = m + 2.
Phương trình có nghiệm ⇔ − 1 ≤ m + 2 ≤ 1 ⇔ − 3 ≤ m ≤ − 1
→ m ∈ ℤ S = − 3 ; − 2 ; − 1 ⇒ T = − 3 + − 2 + − 1 = − 6.
Chọn đáp án B.
Cho phương trình sin x 1 + cos x = 0. Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn [0;2018 π ]. Tìm số phần tử của tập T.
![]()
![]()
![]()
![]()
Cho phương trình  Gọi S là tập hợp tất cả các giá trị thực của
α
thuộc đoạn
0
;
2
π
để phương trình có nghiệm. Tổng các phần tử của tập S bằng
Gọi S là tập hợp tất cả các giá trị thực của
α
thuộc đoạn
0
;
2
π
để phương trình có nghiệm. Tổng các phần tử của tập S bằng
A. π
B. 2
C. 4 π
D. 6 π
Biết S= (a;b) là tập tất cả các giá trị thực của m để phương trình cos3x - cos2x+ mcosx-1 = 0 có đúng 8 nghiệm thực phân biệt thuộc khoảng - π 2 ; 2 π .Tính tổng T = a+b.
A. 4..
B. -2
C. 17 4
D. 25 4
Biết S=(a;b) là tất cả các giá trị thực của m để phương trình
cos
3
x
-
cos
2
x
+
m
cos
x
-
1
=
0
có đúng 8 nghiệm thực phân biệt thuộc khoảng 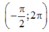 . Tính tổng T=a+b
. Tính tổng T=a+b
A. 4
B. -2
C. 17 4
D. 25 4
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x 3 - 3 x 2 tại 3 điểm phân biệt A, B, C (B nằm giữa A và C) sao cho AB=2BC. Tính tổng các phần tử thuộc
A. -2
B. -4
C. 0
D. 7 - 7 7
Cho phương trình sin x 1 + cos x = 0 . Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn 0 ; 2018 π . Tìm số phần tử của tập T
A. 2019
B. 1009
C. 1010
D. 2018
cho hàm số \(\dfrac{-x+2}{x-1}\) có đồ thị (C) và điểm A(a;1) . Gọi S là tập hợp tất cả các giá trị thực củ tham số a để có đúng 1 tiếp tuyến của (C) đi qua A. Tổng tất cả các giá trị của S là
Cho tập hợp S = 1 , 2 , 3 , 4 , 5 , 6 Gọi M là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau lấy từ S sao cho tổng chữ số các hàng đơn vị, hàng chục và hàng trăm lớn hơn tổng chữ số các hàng còn lại là 3. Tính tổng T của các phần tử của tập hợp M.
![]()
![]()
![]()
![]()