Các câu hỏi tương tự
Cho số phức
z
1
+
3
i
. Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.
Đọc tiếp
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.
![]()
![]()
![]()
![]()
Cho các số phức z1,z2 có điểm biểu diễn trên mặt phẳng tọa độ lần lượt là M,N. Gọi P là trung điểm của MN, khi đó P biểu diễn số phức A.. B.. C.. D..
Đọc tiếp
Cho các số phức z1,z2 có điểm biểu diễn trên mặt phẳng tọa độ lần lượt là M,N. Gọi P là trung điểm của MN, khi đó P biểu diễn số phức
A.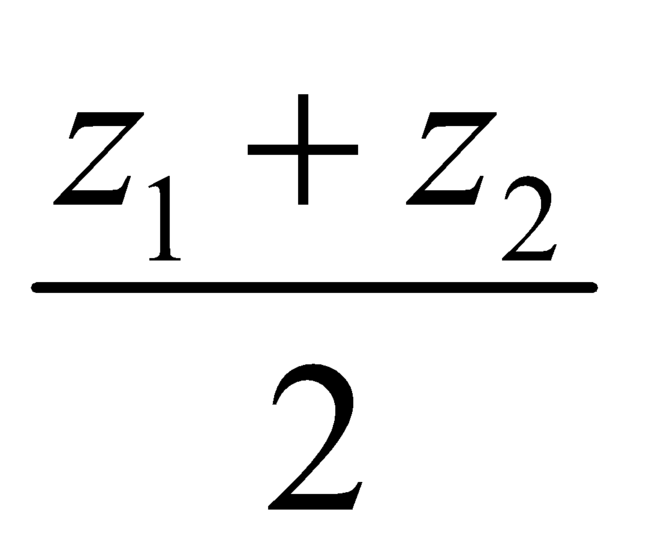 .
.
B.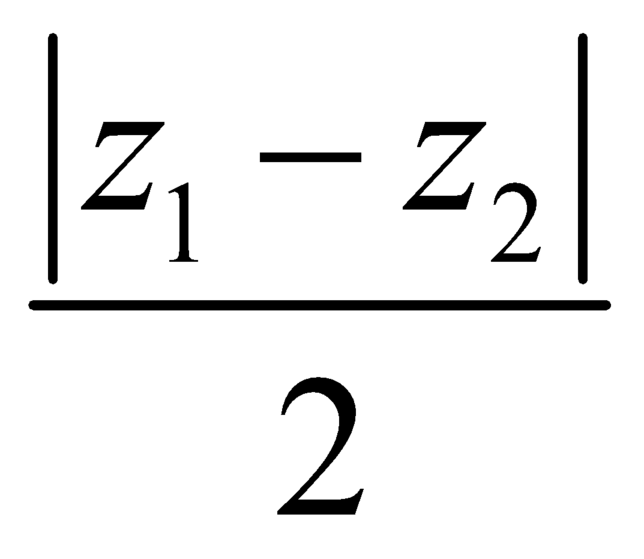 .
.
C.![]() .
.
D.![]() .
.
Gọi A là điểm biểu diễn của số phức
z
-
2
+
5
i
và B là điểm biểu diễn của số phức
z
-
5
+
2
i
trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
Đọc tiếp
Gọi A là điểm biểu diễn của số phức z = - 2 + 5 i và B là điểm biểu diễn của số phức z ' = - 5 + 2 i trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
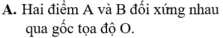
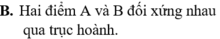
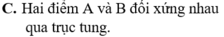
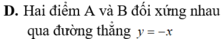
Cho số phức z thỏa mãn
z
+
3
i
+
z
-
3
i
10
. Gọi
M
1
;
M
2
lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của
M
1...
Đọc tiếp
Cho số phức z thỏa mãn z + 3 i + z - 3 i = 10 . Gọi M 1 ; M 2 lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của M 1 M 2 , M(a, b) biểu diễn số phức w, tổng a + b nhận giá trị nào sau đây?
A. 7 2
B. 5
C. 4
D. 9 2
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức
z
1
2
-
i
,
z
2
1
+
4
i
Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
Đọc tiếp
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức z 1 = 2 - i , z 2 = 1 + 4 i Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
![]()
![]()
![]()
![]()
Gọi M là điểm biểu diễn của số phức z, N là điểm biểu diễn của số phức w trong mặt phẳng tọa độ. Biết N là điểm đối xứng với M qua trục Oy (M, N không thuộc các trục tọa độ). Mệnh đề nào sau đây đúng?
Đọc tiếp
Gọi M là điểm biểu diễn của số phức z, N là điểm biểu diễn của số phức w trong mặt phẳng tọa độ. Biết N là điểm đối xứng với M qua trục Oy (M, N không thuộc các trục tọa độ). Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho số phức z1, z2 thỏa mãn
z
1
z
2
2
5
. Gọi M, N lần lượt là điểm biểu diễn hai số phức z1, z2 trên mặt phẳng tọa độ. Biết
M
N
2
2
. Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là trung điểm của OM. Tính lKH.
Đọc tiếp
Cho số phức z1, z2 thỏa mãn z 1 = z 2 = 2 5 . Gọi M, N lần lượt là điểm biểu diễn hai số phức z1, z2 trên mặt phẳng tọa độ. Biết M N = 2 2 . Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là trung điểm của OM. Tính l=KH.
![]()
![]()
![]()
![]()
Gọi điểm A,B lần lượt biểu diễn các số phức z và
z
1
+
i
2
z
;
(z khác 0) trên mặt phẳng tọa độ (A,B,C và A,B,C đều không thẳng hàng). Với O là gốc tọa độ, khẳng định nào sau đây đúng? A. Tam giác OAB đều B. Tam giác OAB vuông cân tại O C. Tam giác OAB vuông cân tại B D. Tam giác OAB vuông cân tại A
Đọc tiếp
Gọi điểm A,B lần lượt biểu diễn các số phức z và z ' = 1 + i 2 z ; (z khác 0) trên mặt phẳng tọa độ (A,B,C và A',B',C' đều không thẳng hàng). Với O là gốc tọa độ, khẳng định nào sau đây đúng?
A. Tam giác OAB đều
B. Tam giác OAB vuông cân tại O
C. Tam giác OAB vuông cân tại B
D. Tam giác OAB vuông cân tại A
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.I(0;-3/2) C.I(0;3/2) D. I(-2;2)
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B.I(0;-3/2)
C.I(0;3/2)
D. I(-2;2)




