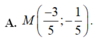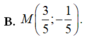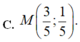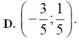Đáp án B
Đặt ![]()
![]()
Ta có:![]()
![]()
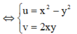
Mà M thuộc đường thẳng d: y = 3x , nên tọa độ của P thỏa mãn
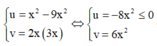
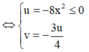
Vậy tập hợp các điểm P là đường thẳng y = - 3 4 x , x ≤ 0
Đáp án B
Đặt ![]()
![]()
Ta có:![]()
![]()
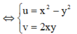
Mà M thuộc đường thẳng d: y = 3x , nên tọa độ của P thỏa mãn
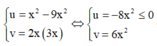
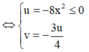
Vậy tập hợp các điểm P là đường thẳng y = - 3 4 x , x ≤ 0
Xét các số phức z=x+yi x , y ∈ R có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình (C): x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
![]()
![]()
![]()
![]()
Tập hợp tất cả các điểm biểu diễn số phức z=x+yi,x,y thuộc R thỏa mãn |z-i|=4 là đường cong có phương trình
A.![]()
B.![]()
C.![]()
D.![]()
Trong không gian Oxyz , cho ba mặt cầu lần lượt có phương trình là ( x + 5 ) 2 + ( y - 1 ) 2 + z 2 = 5 ; x 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 6 và ( x + 1 ) 2 + y 2 + ( z - 4 ) 2 = 9 . Gọi M là điểm di động ở ngoài ba mặt cầu và X, Y , Z là các tiếp điểm của các tiếp tuyến vẽ từ M đến ba mặt cầu. Giả sử MX = MY = MZ , khi đó tập hợp các điểm M là đường thẳng có vectơ chỉ phương là
![]()
![]()
![]()
![]()
z = -1 + i được biểu diễn bởi điểm M trong mặt phẳng Oxy. Biết điểm M' biểu diễn số phức w và M’ đối xứng với M qua đường thẳng: ∆ : x-y+1 = 0. Tìm w.
A. w = 0
B. w = 1-i
C. w = 1+i
D. w = -2+2i
Cho z là số phức thay đổi thỏa mãn ( 1 + i ) z + 2 - i = 4 và M(x,y) là điểm biểu diễn cho z trong mặt phẳng phức. Tìm giá trị lớn nhất của biểu thức T = x + y + 3
A. T = 4 + 2 2
B. 8
C. 4
D. 4 2
Biết {M} biểu diễn số phức Z là (d): x-y-2 = 0. Đặt W = Z+1-i. Tìm W m i n
A. W m i n = 2
B. W m i n = 2
C. W m i n = 2 2
D. W m i n = 4
Cho số phức z = x + y i với x ; y ∈ R thỏa mãn z - 1 - i ≥ 1 và z - 3 - 3 i ≤ 5 . Gọi m; M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = x+2y. Tính tỉ số M m
A. 9 4
B. 7 2
C. 5 4
D. 14 5
Cho các số phức z 1 = 1 + 3 i , z 2 = 5 - 3 i Tìm điểm M(x;y)biểu diễn số phức z 3 , biết rằng trong mặt phẳng phức điểm M nằm trên đường thẳng x - 2y + 1 = 0 và mô đun số phức w = 3 z 3 - z 2 - 2 z 1 đạt giá trị nhỏ nhất.
![]()
![]()
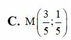
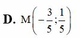
Cho các số phức z 1 = 1 + 3 i , z 2 = - 5 - 3 i Tìm điểm M (x; y) biểu diễn số phức z3, biết rằng trong mặt phẳng phức điểm M nằm trên đường thẳng x - 2y + 1 = 0 và mô đun số phức w = 3 z 3 - z 2 - 2 z 1 đạt giá trị nhỏ nhất.