Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và điểm không xác định của y’
- Tính các giá trị tại 1 e 2 , tại , tại nghiệm của y’ . Tìm GTLN, GTNN trong các giá trị đó. e
- Tính tích M.m.
Cách giải:
TXĐ: D = (0;+∞)
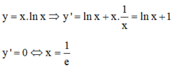
Ta có:
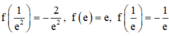
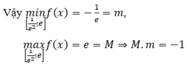
Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và điểm không xác định của y’
- Tính các giá trị tại 1 e 2 , tại , tại nghiệm của y’ . Tìm GTLN, GTNN trong các giá trị đó. e
- Tính tích M.m.
Cách giải:
TXĐ: D = (0;+∞)
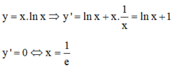
Ta có:
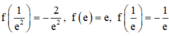
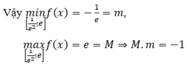
Cho hàm số y = x 2 - 3 x + 3 x - 1 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn - 1 ; 1 2 . Tính tích M.m.
A. - 1 2
B. -3
C. 21 2
D. 0
Gọi M,m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 1 x - 2 trên tập hợp D = ( - ∞ ; - 1 ] ∪ 1 ; 3 2 Khi đó T = m.M bằng
A. 1 9
B. 0
C. 3 2
D. - 3 2
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 3 x + 6 x - 2 trên đoạn [0;1]. Giá trị của M + 2m bằng
A. -11
B. -10
C. 11
D. 10
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f x = x 3 - 3 x 2 + 4 trên đoạn [1; 4]. Giá trị của M + m bằng:
A. 6
B. 18
C. 20
D. 22
Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin2x - cosx + 1 thì M.m bằng
A. 0
B. 25 8
C. 25 4
D. 2
Gọi M; N lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số y = ln ( x + x 2 + 4 ) trên đoạn [0;5] Khi đó tổng M+N là
A. ![]()
B. 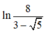
C. ![]() .
.
D. Kết quả khác
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - x 4 + x 2 - 1 trên đoạn [-2;1]. Tính M + m.
A. 0.
B. -9.
C. -10.
D. -1.