Các câu hỏi tương tự
Gọi S là tập hợp tất cả các giá trị của m để đồ thị hàm số
y
x
4
-
2
mx
2
+
2
m
+
m
4
có 3 điểm cực trị đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng 1. Tính tổng các phần tử của S. A. B. C. 0 D.
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị của m để đồ thị hàm số y = x 4 - 2 mx 2 + 2 m + m 4 có 3 điểm cực trị đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng 1. Tính tổng các phần tử của S.
A.
B.
C. 0
D.
Gọi S là tập hợp tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng 1. Tính tổng các phần tử của S.
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị của m để đồ thị hàm số 
có 3 điểm cực trị đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng 1. Tính tổng các phần tử của S.
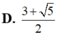
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
4
-
2
m
x
2
+
m
có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn nội tiếp lớn hơn 1 A. m -1 B. m 2 C. ...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 4 - 2 m x 2 + m có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn nội tiếp lớn hơn 1
A. m < -1
B. m > 2
C. m ∈ ( - ∞ , - 1 ) ∪ ( 2 ; + ∞ )
D. Không tồn tại m
Gọi
m
0
là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số
y
x
3
-
6
m
x
+
4
cắt đường tròn tâm I(1;0), bán kính bằng
2
tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau...
Đọc tiếp
Gọi m 0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số y = x 3 - 6 m x + 4 cắt đường tròn tâm I(1;0), bán kính bằng 2 tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
4
-
2
m
x
2
+
m
-
1
có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1 C. ...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 4 - 2 m x 2 + m - 1 có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1
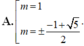
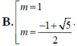
C. m = ± - 1 + 5 2
D. m = 1
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
4
-
2
m
x
2
+
m
-
1
có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1 C. ...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 4 - 2 m x 2 + m - 1 có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1
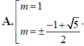
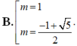
C. m = ± - 1 + 5 2
D. m = 1
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số:
y
x
3
-
3
m
x
+
2
cắt đường tròn tâm
I
(
1
;
1
)...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x 3 - 3 m x + 2 cắt đường tròn tâm I ( 1 ; 1 ) bán kính bằng 1 tại 2 điểm A , B mà diện tích tam giác I A B lớn nhất
A. m = 1 ± 2 2
B. m = 1 ± 3 2
C. m = 1 ± 5 2
D. m = 1 ± 6 2
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y x3-3mx+ 2 cắt đường tròn tâm I (1; 1) bán kính bằng 1 tại 2 điểm A và B mà diện tích tam giác IAB lớn nhất .
A
.
m
1
±
2
2
.
B
.
m
1
±
3...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x3-3mx+ 2 cắt đường tròn tâm I (1; 1) bán kính bằng 1 tại 2 điểm A và B mà diện tích tam giác IAB lớn nhất .
A . m = 1 ± 2 2 .
B . m = 1 ± 3 2 .
C . m = 1 ± 5 2 .
D . m = 1 ± 6 2 .
Cho hàm số
y
x
-
2
x
+
1
có đồ thị (C) . Phương trình tiếp tuyến
∆
của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến
∆
bằng?
A
....
Đọc tiếp
Cho hàm số y = x - 2 x + 1 có đồ thị (C) . Phương trình tiếp tuyến ∆ của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến ∆ bằng?
A . 3
B . 2 6
C . 2 3
D . 6