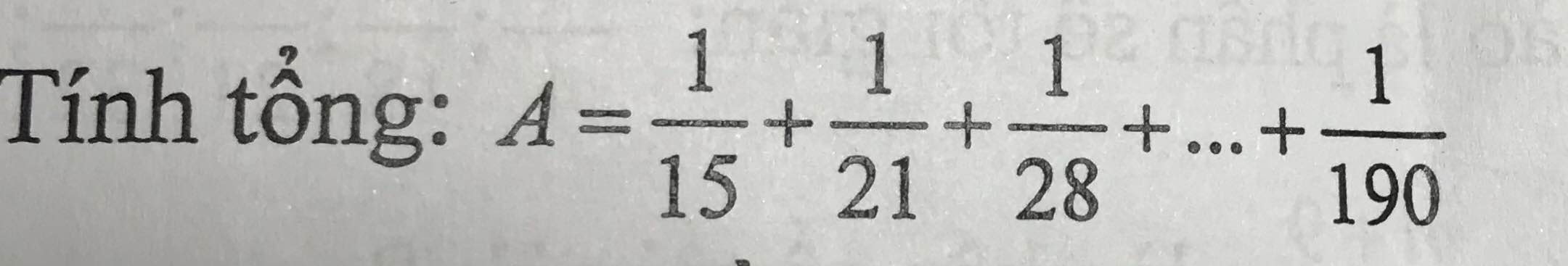Ta có: \(A=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(=\dfrac{1}{2}\left(\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+...+\dfrac{1}{380}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{5}-\dfrac{1}{20}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{4}{20}-\dfrac{1}{20}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{20}=\dfrac{3}{40}\)
Đúng 1
Bình luận (0)
