Ta có: \(a^3+b^3+c^3=\left(a+b+c\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Khi đó: \(\left(x-y\right)^3+\left(y-z\right)^3+\left(z-x\right)^3=\left(x-y+y-z+z-x\right)^3-3\left(x+z-2y\right)\left(y+x-2z\right)\left(z+y-2x\right)=-3\left(x+z-2y\right)\left(y+x-2z\right)\left(z+y-2x\right)=\)
Vậy ta cần chứng minh \(\left(x+z-2y\right)\left(y+x-2z\right)\left(z+y-2x\right)⋮27\)
Ta có: \(\left(x-y\right)\left(y-z\right)\left(z-x\right)=x+y+z\). Xét 2 trường hợp:
+Trường hợp 1: x,y,z có các số dư khác nhau khi chia cho 3. Không mất tính tổng quát, giả sử \(\left\{{}\begin{matrix}x\equiv0\left(mod3\right)\\y\equiv1\left(mod3\right)\\z\equiv2\left(mod3\right)\end{matrix}\right.\). Khi đó \(\left(x+y+z\right)⋮3\).
Mặt khác, để ý \(\left(x-y\right),\left(y-z\right),\left(z-x\right)⋮̸3\), nên \(\left(x-y\right)\left(y-z\right)\left(z-x\right)⋮̸3\)
(mâu thuẫn). Vậy trường hợp này không tồn tại.
+Trường hợp 2: 2 trong 3 số x,y,z có cùng số dư khi chia cho 3. Không mất tính tổng quát, giả sử 2 số đó là x,y. Khi đó \(\left(x-y\right)⋮3\) \(\Rightarrow\left(x+y+z\right)⋮3\).
\(\Rightarrow\left(x-y+x+y+z\right)⋮3\Rightarrow\left(2x+z\right)⋮3\Rightarrow\left(-3x+2x+z\right)⋮3\Rightarrow\left(z-x\right)⋮3\)
Vậy x,y,z có cùng số dư khi chia cho 3. Khi đó: \(\left\{{}\begin{matrix}\left(x+z-2y\right)⋮3\\\left(y+x-2z\right)⋮3\\\left(y+z-2x\right)⋮3\end{matrix}\right.\Rightarrow\left(x+z-2y\right)\left(y+x-2z\right)\left(z+y-2x\right)⋮27\)
\(\Rightarrowđpcm\)

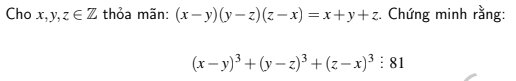







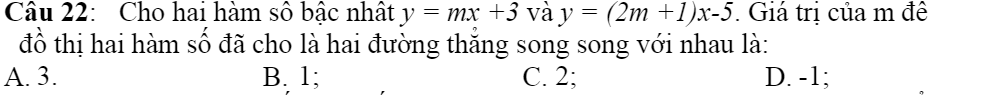
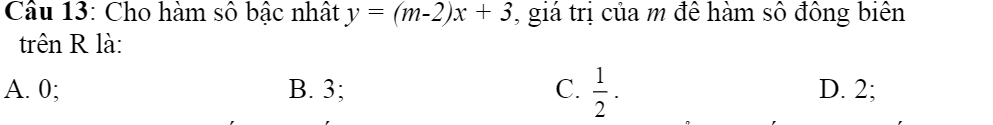
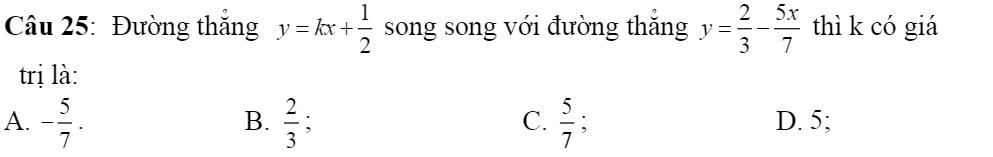
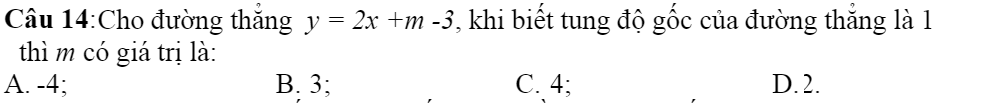

 Giups mình với
Giups mình với
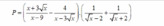
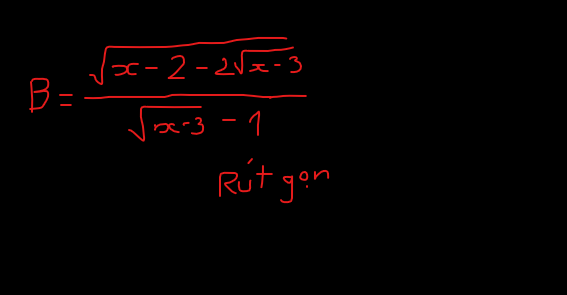


 giups mk voi
giups mk voi 

