a. \(\dfrac{2^{11}.9^2}{3^5.16^2}\)
= \(\dfrac{1^{11}.3^2}{1^5.8^2}\)
= \(\dfrac{9}{64}\)
\(\dfrac{2^{11}.9^2}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^2}{3^5.\left(2^4\right)^2}=\dfrac{8}{3}\)
\(\dfrac{9^3.27^2}{6^2.3^{10}}=\dfrac{\left(3^2\right)^3.\left(3^3\right)^2}{\left(2.3\right)^2.3^{10}}=\dfrac{1}{2}\)
\(\dfrac{27^{15}.5^3.8^4}{25^2.81^{11}.2^{11}}=\dfrac{\left(3^3\right)^{15}.5^3.\left(2^3\right)^4}{\left(5^2\right)^2.\left(3^4\right)^{11}.2^{11}}=\dfrac{3.2}{5}=\dfrac{6}{5}\)
a:\(\dfrac{2^{11}\cdot9^2}{3^5\cdot16^2}=\dfrac{2^{11}\cdot3^4}{3^5\cdot2^8}=\dfrac{2^3}{3}=\dfrac{8}{3}\)
b: \(\dfrac{9^3\cdot27^2}{6^2\cdot3^{10}}=\dfrac{3^6\cdot3^6}{3^2\cdot3^{10}\cdot2^2}=\dfrac{1}{4}\)
c: \(\dfrac{27^{15}\cdot5^3\cdot8^4}{25^2\cdot81^{11}\cdot2^{11}}=\dfrac{3^{45}\cdot5^3\cdot2^{12}}{5^4\cdot3^{44}\cdot2^{11}}=\dfrac{1}{5}\cdot3\cdot2=\dfrac{6}{5}\)

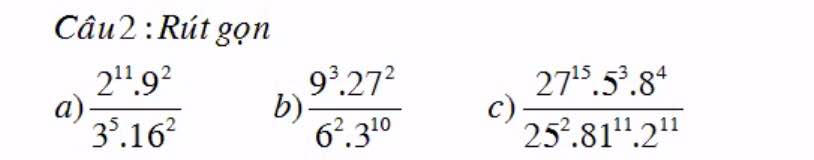

















 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ