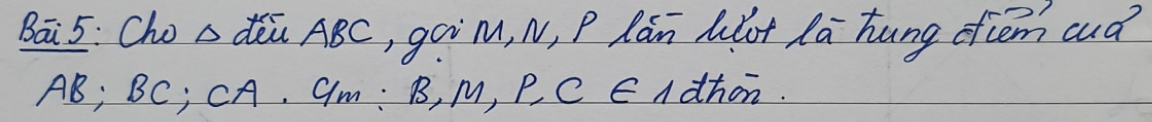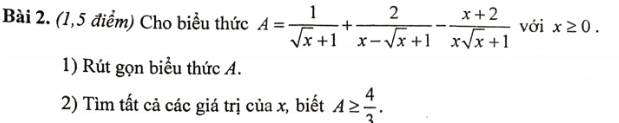Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{13}{2}\\x_1x_2=-3\end{matrix}\right.\)
\(A=x_1^2+2x_2^2+3x_1x_2-x_2^2=x_1^2+x_2^2+2x_1x_2+x_1x_2\)
\(=\left(x_1+x_2\right)^2+x_1x_2\)
\(=\left(\dfrac{13}{2}\right)^2-3=...\)
Theo Vi-et, ta có:
\(x_1+x_2=-\dfrac{\left(-13\right)}{2}=\dfrac{13}{2};x_1x_2=\dfrac{c}{a}=-\dfrac{6}{2}=-3\)
\(\left(x_1+x_2\right)\left(x_1+2x_2\right)-x_2^2\)
\(=x_1^2+2x_1x_2+x_1x_2+2x_2^2-x_2^2\)
\(=x_1^2+3x_1x_2+x_2^2\)
\(=\left(x_1+x_2\right)^2+x_1x_2\)
\(=\left(\dfrac{13}{2}\right)^2+\left(-3\right)=\dfrac{169}{4}-3=\dfrac{157}{4}\)
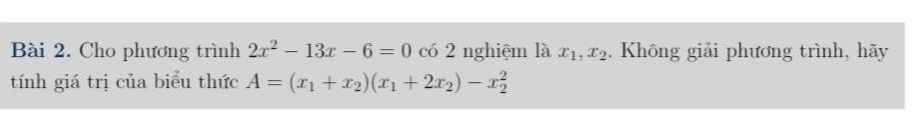
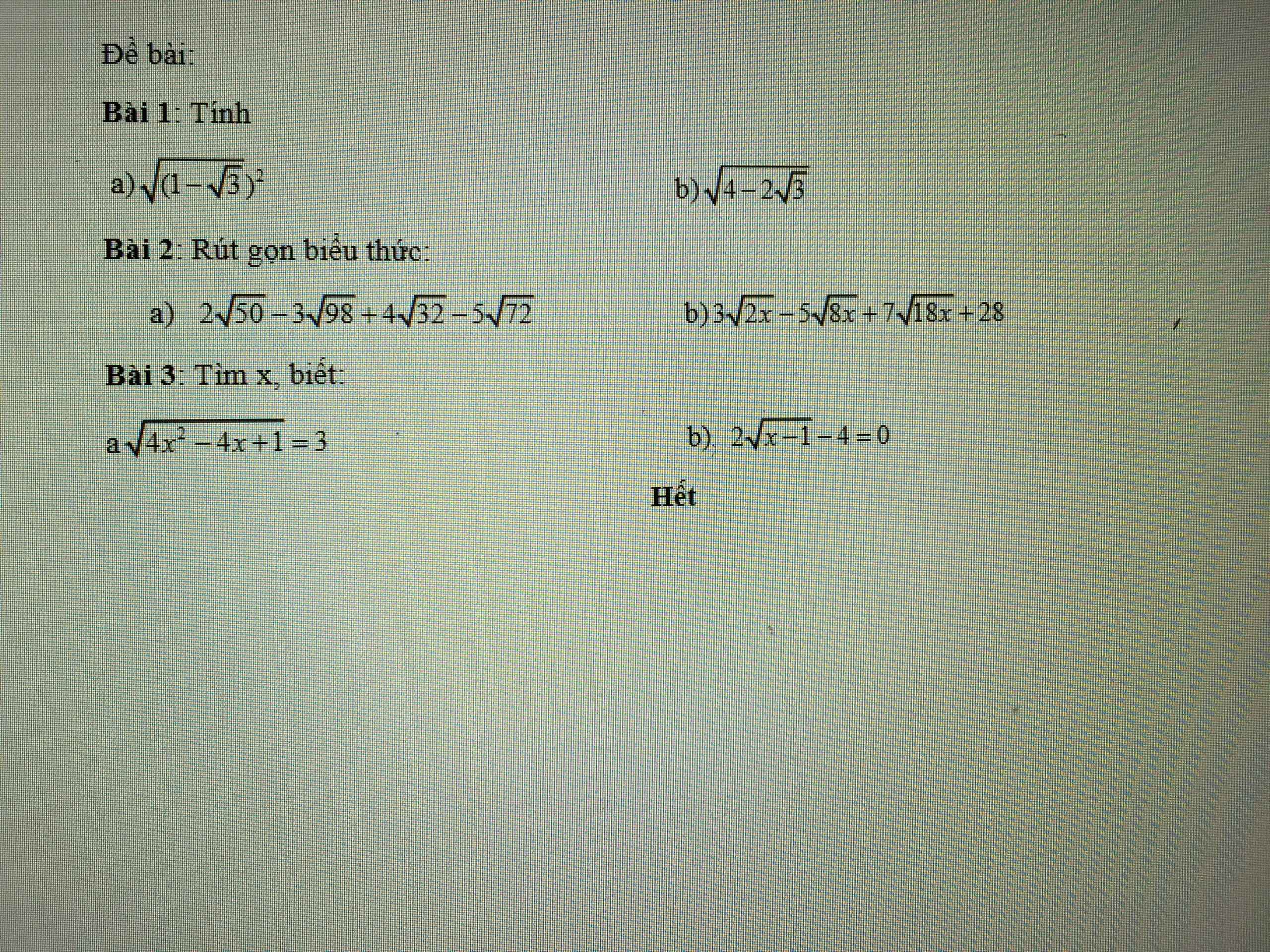Giúp mình vs ạ. Cảm ơn trước ạ!
