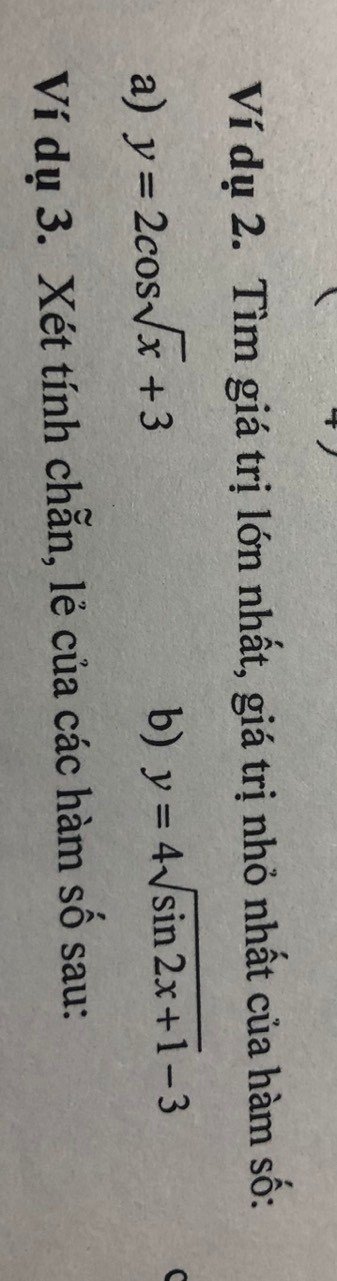a: ĐKXĐ: \(\sqrt{x}\ge0\)
=>x>=0
Ta có: \(-1\le cos\sqrt{x}\le1\)
=>\(-2\le2\cdot cos\sqrt{x}\le2\)
=>\(-2+3\le2\cdot cos\sqrt{x}+3\le2+3\)
=>1<=y<=5
Do đó: \(y_{\min}=1\) khi \(cos\sqrt{x}=-1\)
=>\(\sqrt{x}=\pi+k2\pi=\pi\left(2k+1\right)\)
=>\(x=\pi^2\cdot\left(2k+1\right)^2\)
\(y_{\max}=5\) khi \(cos\sqrt{x}=1\)
=>\(\sqrt{x}=k2\pi\)
=>\(x=\left(k2\pi\right)^2=4k^2\cdot\pi^2\)
b: \(-1\le\sin2x\le1\)
=>\(-1+1\le\sin2x+1\le1+1\)
=>\(0\le\sin2x+1\le2\)
=>\(0\le\sqrt{\sin2x+1}\le\sqrt2\)
=>\(0\le4\cdot\sqrt{\sin2x+1}\le4\sqrt2\)
=>\(0-3\le4\cdot\sqrt{\sin2x+1}-3\le4\sqrt2-3\)
=>-3<=y<=\(4\sqrt2-3\)
Do đó: \(y_{\min}=-3\) khi sin 2x=-1
=>\(2x=-\frac{\pi}{2}+k2\pi\)
=>\(x=-\frac{\pi}{4}+k\pi\)
\(y_{\max}=4\sqrt2-3\) khi sin 2x=1
=>\(2x=\frac{\pi}{2}+k2\pi\)
=>\(x=\frac{\pi}{4}+k\pi\)