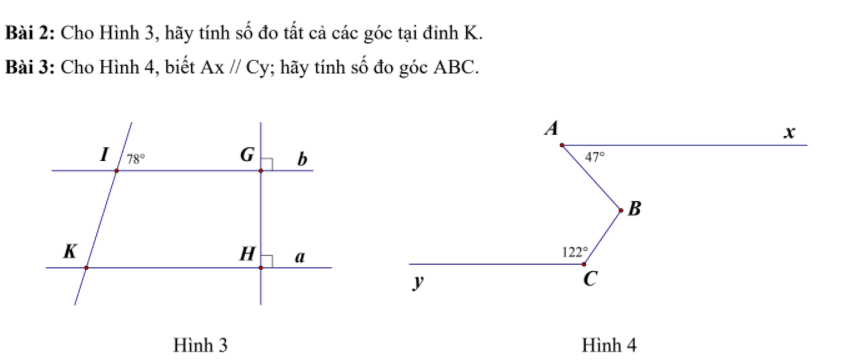
Bài 2:
Vì $b\perp GH, a\perp GH\Rightarrow a\parallel b$
Do đó:
$\widehat{K_1}=\widehat{I_1}=78^0$ (hai góc đồng vị)
$\widehat{K_2}=\widehat{K_1}=78^0$ (hai góc đối đỉnh)
$\widehat{K_4}=180^0-\widehat{K_1}=180^0-78^0=102^0$ (hai góc kề bù)
$\widehat{K_3}=\widehat{K_4}=102^0$ (đối đỉnh)
Bài 3: Kẻ tia $Bt\parallel Ax$. Vì $Ax\parallel Cy$ nên $Bt\parallel Cy$
Ta có:
$\widehat{B_1}=\widehat{BAx}=47^0$ (hai góc so le trong)
$\widehat{B_2}+\widehat{BCy}=180^0$ (trong cùng phía)
$\Rightarrow \widehat{B_2}=180^0-\widehat{BCy}=180^0-122^0=58^0$
Do đó: $\widehat{ABC}=\widehat{B_1}+\widehat{B_2}=47^0+58^0=105^0$



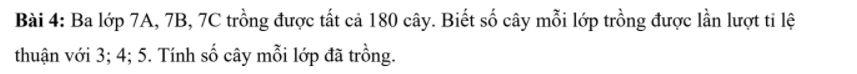
 giúp tớ tớ cần gấp
giúp tớ tớ cần gấp
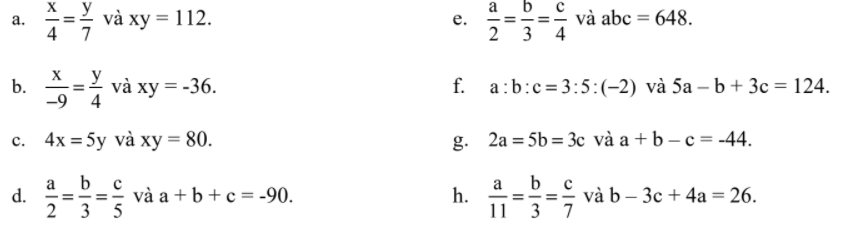



 giúp tớ với tớ cần gấp
giúp tớ với tớ cần gấp