a) Để tính tích bc, ah, ch, bh, ta sử dụng các quy tắc trong tam giác vuông.
- Tích bc: Tích bc là tích của hai cạnh góc vuông AB và AC. Vì AB = 6 và AC = 8, nên tích bc = AB * AC = 6 * 8 = 48.
- Đường cao ah: Đường cao ah là đường thẳng đi qua đỉnh A và vuông góc với cạnh BC. Trong tam giác vuông ABC, đường cao ah chính là cạnh huyền AB. Vì vậy, ah = AB = 6.
- Cạnh ch: Cạnh ch là cạnh góc vuông AC. Vì AC = 8, nên ch = AC = 8.
- Cạnh bh: Cạnh bh là cạnh góc vuông BC. Vì BC là cạnh huyền của tam giác vuông ABC, nên bh = BC = 10 (theo định lý Pythagoras).
b) Khi qua C kẻ đường thẳng vuông góc với bc, đường thẳng này cắt tia BA tại K. Ta cần tính ck.
- Đường thẳng vuông góc với bc: Đường thẳng vuông góc với bc là đường thẳng đi qua điểm C và vuông góc với cạnh BC. Vì BC là cạnh huyền của tam giác vuông ABC, nên đường thẳng này cắt BC tại trung điểm M của BC.
- Tia BA: Tia BA là tia đi qua điểm B và đi qua điểm A.
- Đường thẳng vuông góc với bc cắt tia BA tại K: Đường thẳng vuông góc với bc cắt tia BA tại K, và CK là đoạn thẳng từ C đến K.
Để tính ck, ta sử dụng định lý Euclid: "Trong một tam giác vuông, đường cao chia cạnh huyền thành hai đoạn thẳng có tích bằng tích của hai cạnh góc vuông".
Vì tích bc = 48 và ch = 8, nên ck = (bc × ch) / ah = (48 × 8) / 6 = 64.
- Từ giác Ahck là hình gì? Vì sao?
Giác Ahck là hình chữ nhật. Vì ah = ck và ch = ah, nên ta có các cạnh liên tiếp của hình chữ nhật là ah, ch, ck và khác nhau hai đôi một. Đồng thời, hai đường chéo của hình chữ nhật Ahck cắt nhau tại trung điểm của chúng, tức là M, là trung điểm của BC. Vì vậy, giác Ahck là hình chữ nhật.
- Diện tích tứ giác ahck:
Diện tích tứ giác ahck là tích của hai cạnh chóp ah và ck. Vì ah = 6 và ck = 64, nên diện tích tứ giác ahck = ah × ck = 6 × 64 = 384.
a) Để tính tích bc, ah, ch, bh, ta sử dụng các quy tắc trong tam giác vuông.
- Tích bc: Tích bc là tích của hai cạnh góc vuông AB và AC. Vì AB = 6 và AC = 8, nên tích bc = AB * AC = 6 * 8 = 48.
- Đường cao ah: Đường cao ah là đường thẳng đi qua đỉnh A và vuông góc với cạnh BC. Trong tam giác vuông ABC, đường cao ah chính là cạnh huyền AB. Vì vậy, ah = AB = 6.
- Cạnh ch: Cạnh ch là cạnh góc vuông AC. Vì AC = 8, nên ch = AC = 8.
- Cạnh bh: Cạnh bh là cạnh góc vuông BC. Vì BC là cạnh huyền của tam giác vuông ABC, nên bh = BC = 10 (theo định lý Pythagoras).
b) Khi qua C kẻ đường thẳng vuông góc với bc, đường thẳng này cắt tia BA tại K. Ta cần tính ck.
- Đường thẳng vuông góc với bc: Đường thẳng vuông góc với bc là đường thẳng đi qua điểm C và vuông góc với cạnh BC. Vì BC là cạnh huyền của tam giác vuông ABC, nên đường thẳng này cắt BC tại trung điểm M của BC.
- Tia BA: Tia BA là tia đi qua điểm B và đi qua điểm A.
- Đường thẳng vuông góc với bc cắt tia BA tại K: Đường thẳng vuông góc với bc cắt tia BA tại K, và CK là đoạn thẳng từ C đến K.
Để tính ck, ta sử dụng định lý Euclid: "Trong một tam giác vuông, đường cao chia cạnh huyền thành hai đoạn thẳng có tích bằng tích của hai cạnh góc vuông".
Vì tích bc = 48 và ch = 8, nên ck = (bc * ch) / ah = (48 * 8) / 6 = 64.
- Từ giác Ahck là hình gì? Vì sao?
Giác Ahck là hình chữ nhật. Vì ah = ck và ch = ah, nên ta có các cạnh liên tiếp của hình chữ nhật là ah, ch, ck và khác nhau hai đôi một. Đồng thời, hai đường chéo của hình chữ nhật Ahck cắt nhau tại trung điểm của chúng, tức là M, là trung điểm của BC. Vì vậy, giác Ahck là hình chữ nhật.
- Diện tích tứ giác ahck:
Diện tích tứ giác ahck là tích của hai cạnh chóp ah và ck. Vì ah = 6 và ck = 64, nên diện tích tứ giác ahck = ah * ck = 6 * 64 = 384.
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>BC=10
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\CH\cdot CB=CA^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\\CH=\dfrac{8^2}{10}=6,4\end{matrix}\right.\)
b: Xét ΔCKB vuông tại C có CA là đường cao
nên \(AK\cdot AB=CA^2\)
=>\(AK\cdot6=8^2=64\)
=>\(AK=\dfrac{64}{6}=\dfrac{32}{3}\)
ΔCKA vuông tại A
=>\(CK^2=CA^2+AK^2\)
=>\(CK^2=\left(\dfrac{32}{3}\right)^2+8^2=\dfrac{1600}{9}\)
=>\(CK=\sqrt{\dfrac{1600}{9}}=\dfrac{40}{3}\)
AH\(\perp\)BC
CK\(\perp\)CB
Do đó: AH//CK
Xét tứ giác AHCK có AH//CK
nên AHCK là hình thang
Hình thang AHCK có \(\widehat{AHC}=90^0\)
nên AHCK là hình thang vuông
=>\(S_{AHCK}=\dfrac{1}{2}\cdot CH\cdot\left(AH+CK\right)\)
\(=\dfrac{1}{2}\cdot6,4\cdot\left(\dfrac{40}{3}+4,8\right)\)
\(=3,2\cdot\dfrac{272}{15}=\dfrac{4352}{75}\)













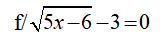
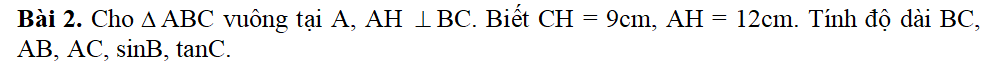



 mn gấp quá có ai giúp em vớiiii
mn gấp quá có ai giúp em vớiiii
