Lời giải:
Nếu $x+y+z+t=0$ thì $M=\frac{-t}{t}=\frac{-x}{x}=\frac{-z}{z}=-1$
$\Rightarrow (M-1)^{2025}=(-1-1)^{2025}=(-2)^{2025}$
Nếu $x+y+z+t\neq 0$. Áp dụng TCDTSBN:
$M=\frac{x+y+z}{t}=\frac{y+z+t}{x}=\frac{z+t+x}{y}=\frac{t+x+y}{z}=\frac{x+y+z+y+z+t+z+t+x+t+x+y}{t+x+y+z}=\frac{3(x+y+z+t)}{x+y+z+t}=3$
$\Rightarrow (M-1)^{2025}=2^{2025}$






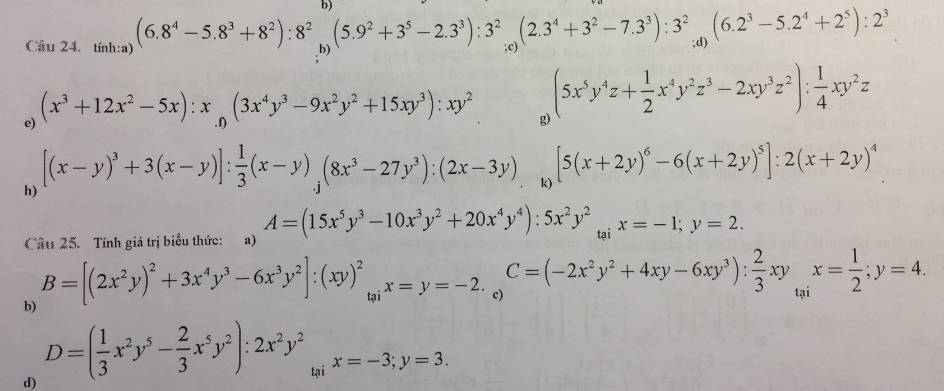
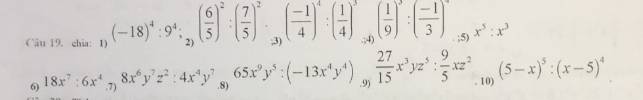 tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
