Question

Giúp tớ lm 2 bài này vs ạ, bài 2 lm phần c th và bài 3 lm phần a và b nho<3 iu nhìu 

Answer 1

Bài 2:
c, Do ΔABI = ΔKBI ⇒ AI = KI (cặp cạnh tương ứng)
Xét ΔAIE và ΔKIC có:
\(\widehat{EAI}=\widehat{CKI}\left(=90^o\right)\)
\(AI=KI\)
\(\widehat{AIE}=\widehat{KIC}\) (đối đỉnh)
⇒ ΔAIE = ΔKIC (c-g-c) 
⇒ \(AE=KC,IE=IC\) (cặp cạnh tương ứng)
Ta có: BE = BA + AE ; BC = BK +KC mà AE = KC, BA = BK
⇒ BE = BC
Xét ΔBEF và ΔBCF có:
BE = BC (cmt)
BF chung
EF = CF (gt)
⇒ ΔBEF = ΔBCF (c-c-c) ⇒ \(\widehat{B_1}=\widehat{B_2}\) (2 góc tương ứng) 
⇒ BF là tia phân giác góc ABC mà BI là tia phân giác góc ABC
⇒ B,I,F thẳng hàng (đpcm)

           

Answer 2

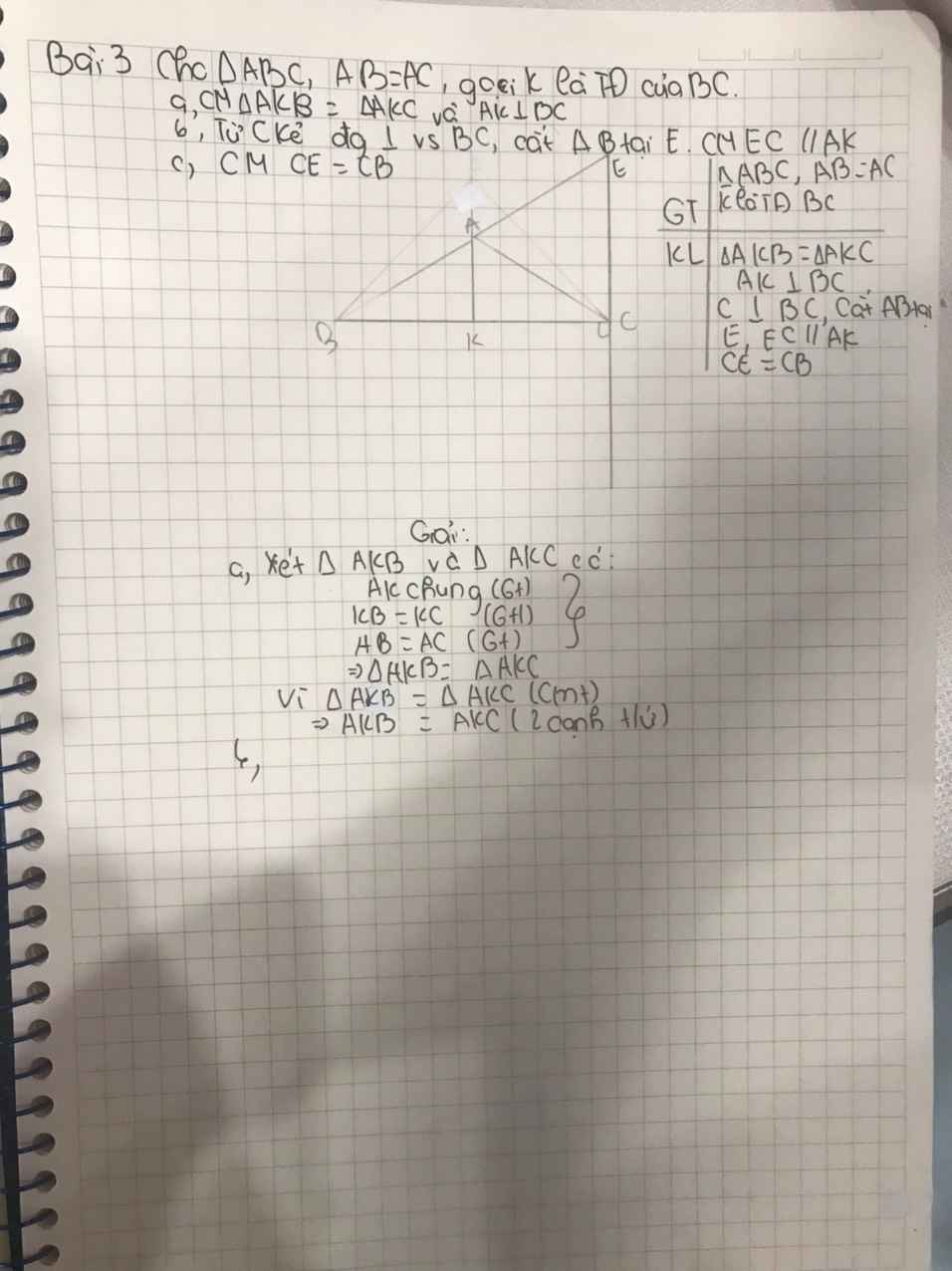
Bài 3:
a, Do H là trung điểm của BC ⇒ AH là đường trung tuyến trong ΔABC mà ΔABC cân tại A (AB=AC) ⇒ AH là đường cao ⇒ AH ⊥ BC (đpcm)
b, Do AH ⊥ BC , lại có: CE ⊥ BC ⇒ CE // AH (tính chất từ vuông góc đến song song) (đpcm)