Câu 3:
a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Ta có: OC là phân giác của góc MOA
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\)
c: Ta có:AC\(\perp\)AB
BD\(\perp\)AB
Do đó: AC//BD
Xét ΔNCA và ΔNBD có
\(\widehat{NCA}=\widehat{NBD}\)(hai góc so le trong, AC//BD)
\(\widehat{CNA}=\widehat{BND}\)(hai góc đối đỉnh)
Do đó: ΔNCA đồng dạng với ΔNBD
=>\(\dfrac{NC}{NB}=\dfrac{AC}{BD}=\dfrac{NA}{ND}\)
=>\(\dfrac{NA}{ND}=\dfrac{MC}{MD}\)
=>\(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
Xét ΔDAC có \(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
nên MN//AC

 Giúp tớ câu 3 với aaa:<
Giúp tớ câu 3 với aaa:<



 Giúp tớ câu 4 hoặc câu 5 với ạ
Giúp tớ câu 4 hoặc câu 5 với ạ




 giúp e gấp với aaa
giúp e gấp với aaa
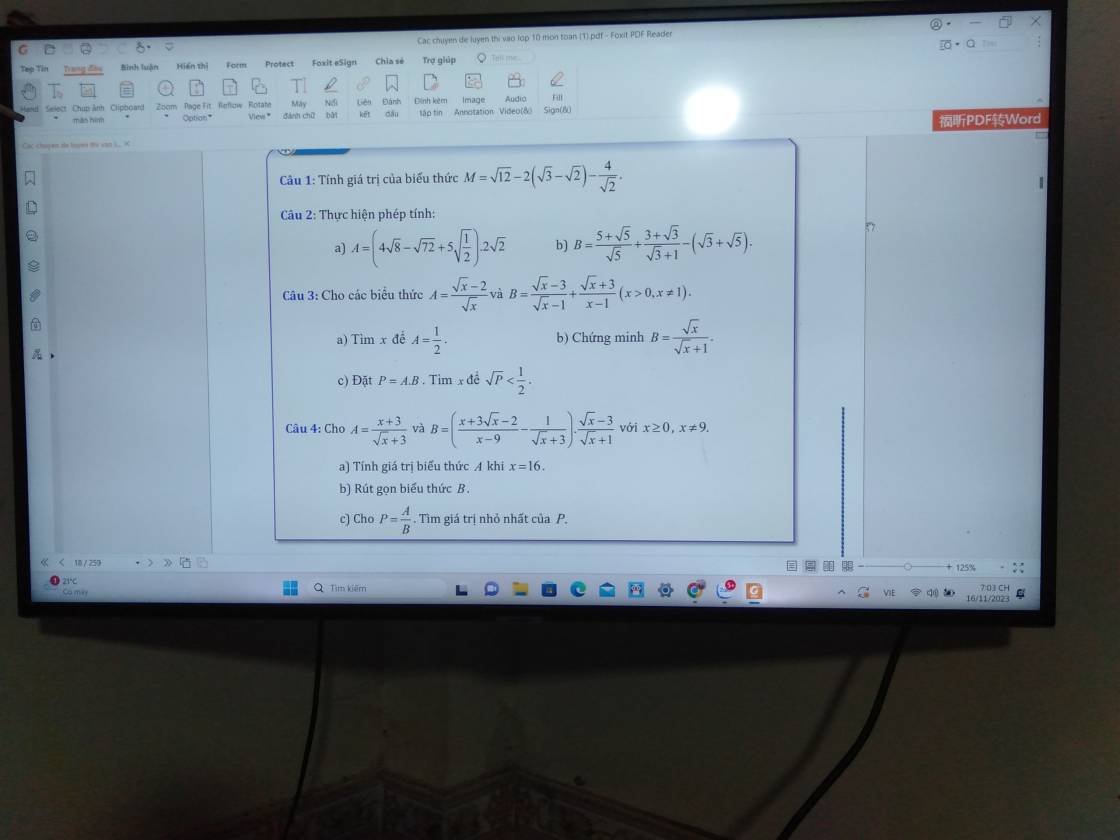
 giúp e với aaa, e cảm ơn
giúp e với aaa, e cảm ơn