1) Ta có: \(x+\dfrac{1}{5}=0.25\)
\(\Leftrightarrow x=\dfrac{1}{4}-\dfrac{1}{5}\)
hay \(x=\dfrac{1}{20}\)
Vậy: \(x=\dfrac{1}{20}\)
2) Ta có: \(\dfrac{2}{7}-\dfrac{3}{7}:x=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{3}{7}:x=\dfrac{2}{7}-\dfrac{1}{5}=\dfrac{3}{35}\)
hay x=5
Vậy: x=5
3) Ta có: \(\left(3x-1.5\right)\left(-\dfrac{1}{2}x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1.5=0\\-\dfrac{1}{2}x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=10\end{matrix}\right.\)
Vậy: \(x\in\left\{\dfrac{1}{2};10\right\}\)
4) Ta có: \(\left(x+3\right)^2-\dfrac{1}{3}=\dfrac{1}{9}\)
\(\Leftrightarrow\left(x+3\right)^2=\dfrac{4}{9}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=\dfrac{2}{3}\\x+3=-\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{3}\\x=-\dfrac{9}{3}\end{matrix}\right.\)
Vậy: \(x\in\left\{-\dfrac{7}{3};-\dfrac{9}{3}\right\}\)
5) Ta có: \(60\%x-x+\dfrac{1}{3}=2\)
\(\Leftrightarrow\dfrac{-2}{5}x=\dfrac{5}{3}\)
hay \(x=-\dfrac{25}{6}\)
Vậy: \(x=-\dfrac{25}{6}\)











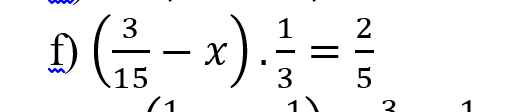 giúp mk với ạ mk cần gấp cho ngày mai
giúp mk với ạ mk cần gấp cho ngày mai
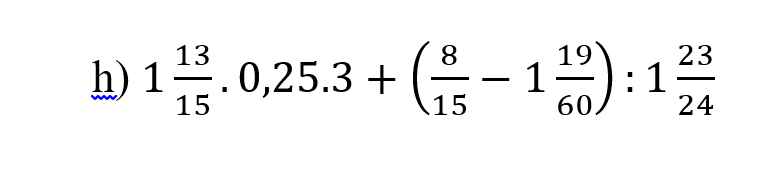 giúp mk với ạ
giúp mk với ạ 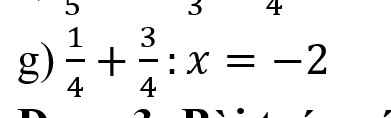 giúp mk với ạ
giúp mk với ạ
 giúp mk c3 với ạ
giúp mk c3 với ạ