`a)sin 2x+2cos x+5sin x+5=0`
`<=>2sin x cos x+2cos x+5sin x+5=0`
`<=>2cos x(sin x+1)+5(sin x+1)=0`
`<=>(sin x+1)(2cos x+5)=0`
`<=>[(sin x=-1),(cos x=-5/2(VN)):}`
`<=>x=-\pi/2+k2\pi` `(k in ZZ)`
__________________________________________
`b)cos^3 x-sin^3 x=cos 2x`
`<=>(cos x-sin x)(cos^2 x+cos x sin x+sin^2 x)=cos^2 x-sin^2 x`
`<=>(cos x-sin x)[1+cos x sin x-(cos x+sin x)]=0`
`<=>(cos x-sin x)(1+cos x sin x-cos x-sin x)=0`
`<=>(cos x-sin x)[1-cos x-sin x(1-cos x)]=0`
`<=>(cos x-sin x)(1-cos x)(1-sin x)=0`
`<=>[(cos x=sin x),(cos x=1),(sin x=1):}`
`<=>[(cos x=cos(\pi/2-x)),(x=k2\pi),(x=\pi/2+k2\pi):}`
`<=>[(x=\pi/2-x+k2\pi<=>x=\pi/2+k\pi),(x=-\pi/2+x+k2\pi<=>0x=-\pi/2+k2\pi(VN)),(x=k2\pi),(x=\pi/2+k2\pi):}`
`<=>[(x=\pi/2+k\pi),(x=k2\pi):}` `(k in ZZ)`
$\begin{array}{l}
\sin 2x + 2\cos x + 5\sin x + 5 = 0\\
\Leftrightarrow 2\sin x\cos x + 2\cos x + 5\left( {\sin x + 1} \right) = 0\\
\Leftrightarrow 2\cos x\left( {\sin x + 1} \right) + 5\left( {\sin x + 1} \right) = 0\\
\Leftrightarrow \left( {\sin x + 1} \right)\left( {2\cos x + 5} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\sin x = - 1\\
\cos x = - \dfrac{5}{2}(L)
\end{array} \right. \Leftrightarrow x = - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\\
b){\cos ^3}x - {\sin ^3}x = \cos 2x\\
\Leftrightarrow \left( {\cos x - \sin x} \right)\left( {{{\cos }^2}x + {{\sin }^2}x + \cos x\sin x} \right) = \left( {\cos x - \sin x} \right)\left( {\cos x + \sin x} \right)\\
\Leftrightarrow \left( {\cos x - \sin x} \right)\left( {1 - \sin x - \cos x - \sin x\cos x} \right) = 0\\
\Leftrightarrow \left( {\cos x - \sin x} \right)\left( {\sin x + \cos x + \sin x\cos x - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\cos x = \sin x\\
\sin x + \cos x + \sin x\cos x = 1
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
\sqrt 2 \cos \left( {x + \dfrac{\pi }{4}} \right) = 0\\
t + \dfrac{{{t^2} - 1}}{2} = 1\left( {t = \sin x + \cos x, - \sqrt 2 \le t \le \sqrt 2 } \right)
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x + \dfrac{\pi }{4} = \dfrac{\pi }{2} + k\pi \\
{t^2} + 2t - 1 = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
t = - 1 - \sqrt 2 (L)\\
t = \sqrt 2 - 1
\end{array} \right.\\
\Rightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
\sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) = \sqrt 2 - 1
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
\sin \left( {x + \dfrac{\pi }{4}} \right) = 1 - \dfrac{{\sqrt 2 }}{2}
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \dfrac{\pi }{4} + k\pi \\
x + \dfrac{\pi }{4} = \arcsin \left( {1 - \dfrac{{\sqrt 2 }}{2}} \right) + k2\pi \\
x + \dfrac{\pi }{4} = \pi - \arcsin \left( {1 - \dfrac{{\sqrt 2 }}{2}} \right) + k2\pi
\end{array} \right.\left( {k \in \mathbb Z} \right)
\end{array}$

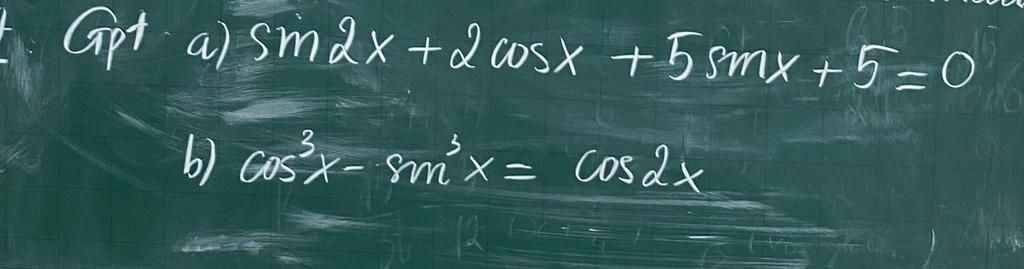
















 giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ




