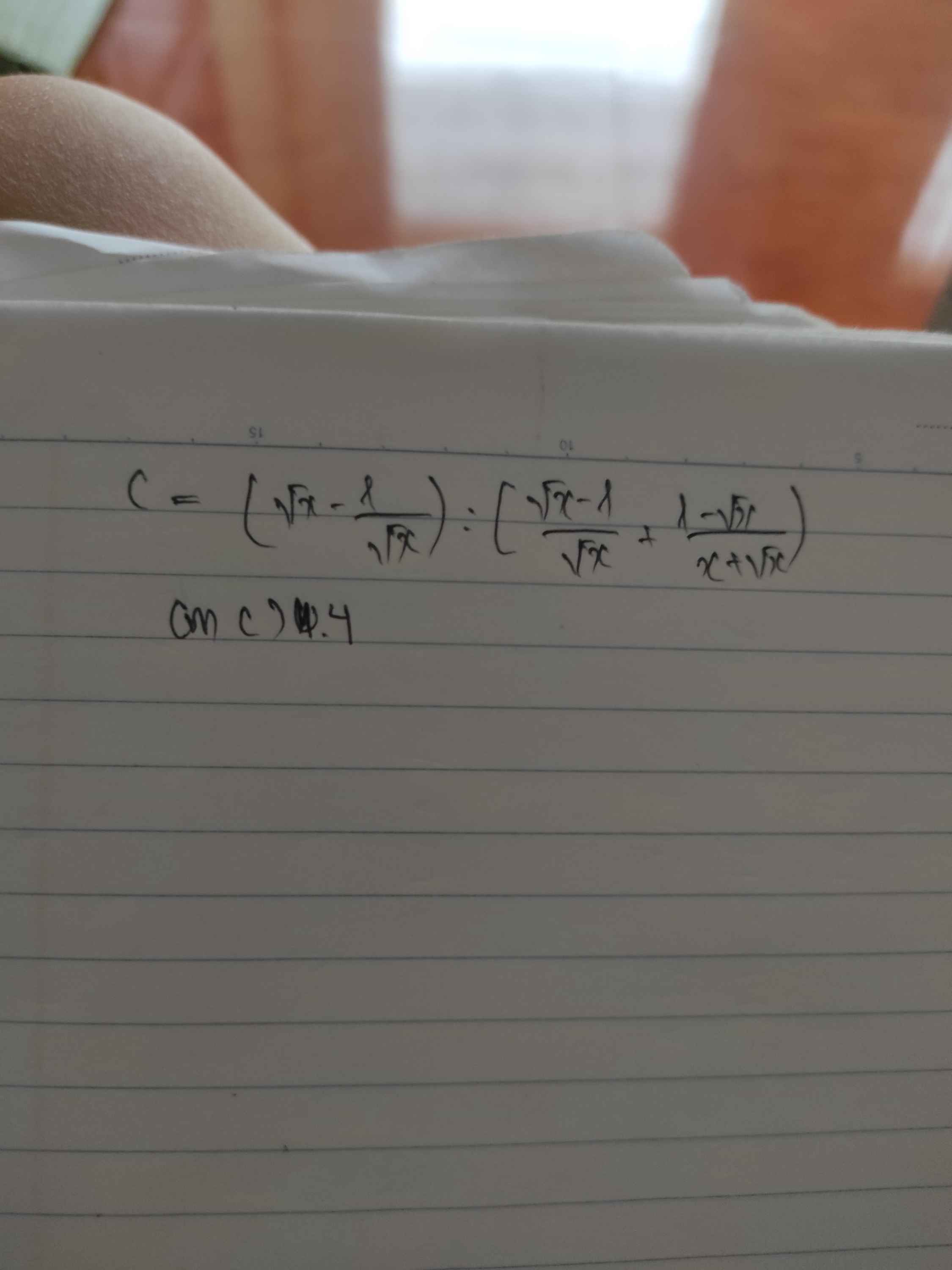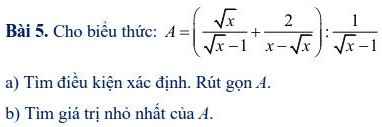\(\left(m-2\right)x^2-\left(2m+5\right)x+m+7=0\left(1\right)\)
\(\Delta=\left(2m+5\right)^2-4\left(m+7\right)\left(m-2\right)\)
\(\Rightarrow\Delta=4m^2+20m+25-4m^2-20m+56=81>0\)
\(\Rightarrow\left(1\right)\) luôn có \(2\) nghiệm phân biệt \(x_1;x_2\)
Theo đề bài ta có :
\(x_1=2x_2\Rightarrow\left\{{}\begin{matrix}x_1+x_2=3x_2=\dfrac{2m+5}{m-2}\\x_1x_2=2x_2^2=\dfrac{m+7}{m-2}\end{matrix}\right.\) (Vi -ét)
\(\Rightarrow\left[\dfrac{\left(2m+5\right)}{3\left(m-2\right)}\right]^2=\dfrac{m+7}{2\left(m-2\right)}\left(m\ne2\right)\)
\(\Leftrightarrow2\left(2m+5\right)^2=9\left(m+7\right)\left(m-2\right)\)
\(\Leftrightarrow8m^2+40m+50=9m^2+45m-126\)
\(\Leftrightarrow m^2-5m-176=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=11\\m=-16\end{matrix}\right.\) thỏa yêu cầu đề bài






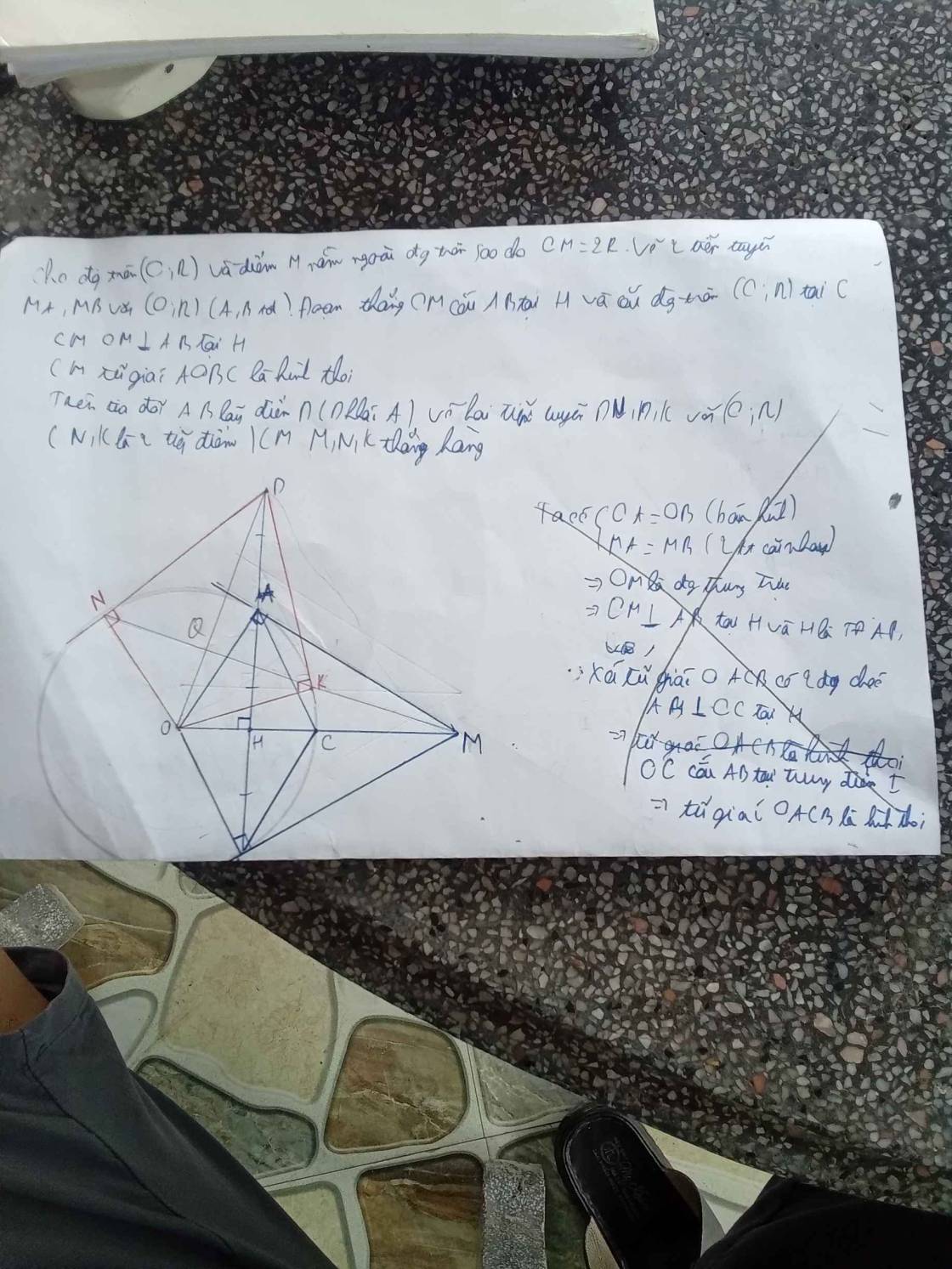
 giúp minh câu c ạ
giúp minh câu c ạ