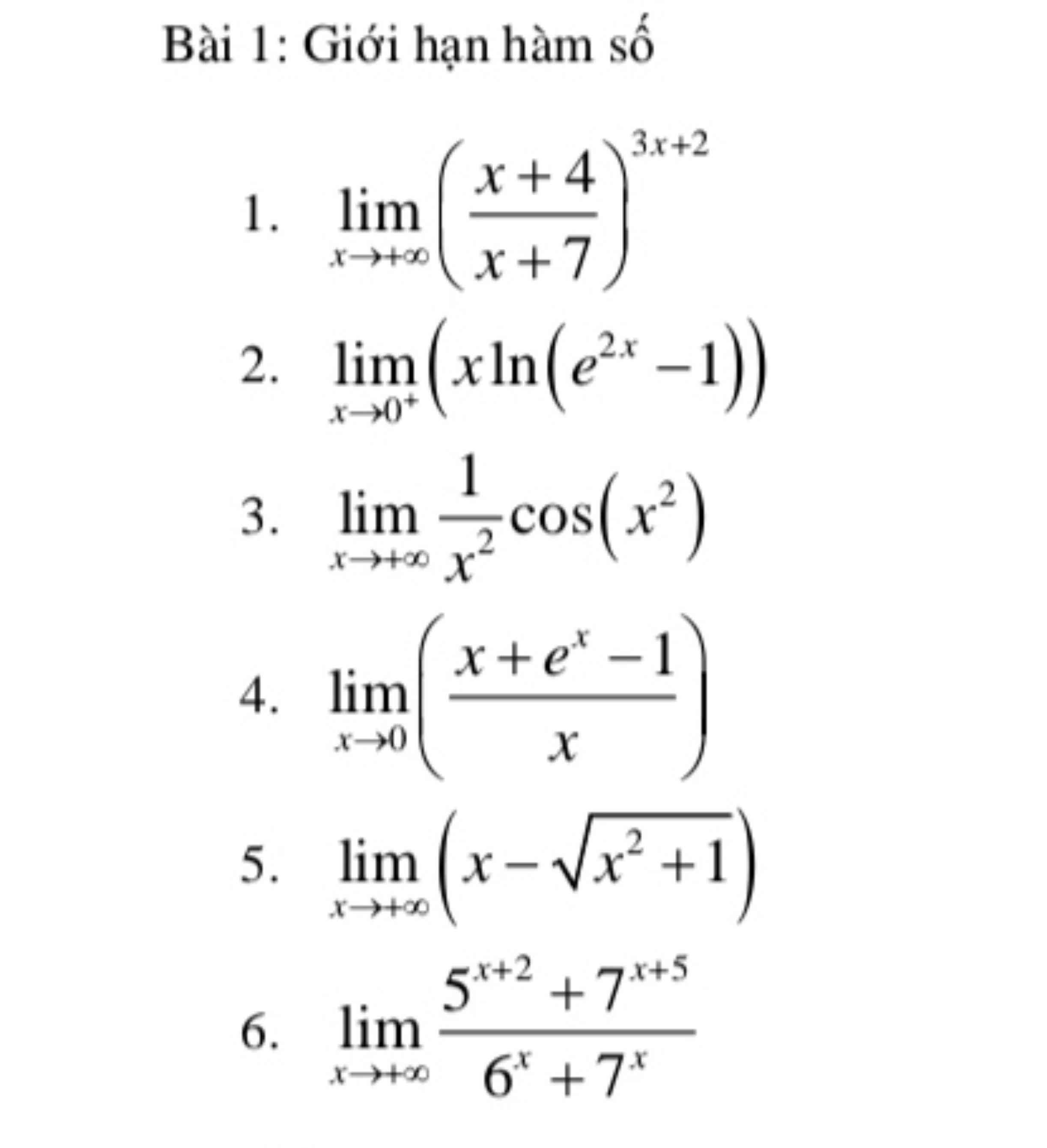a.
\(=\lim\limits _{x\rightarrow +\infty }\left( 1+\dfrac{-3}{x+7}\right)^{\frac{x+7}{-3}.\frac{-3(3x+2)}{x+7}}=e^{-3.3}=e^{-9}=\dfrac{1}{e^9}\)
b.
\(=\lim\limits_{x\rightarrow0^+}\dfrac{ln\left(e^{2x}-1\right)}{\dfrac{1}{x}}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2.e^{2x}}{e^{2x}-1}}{-\dfrac{1}{x^2}}=\lim\limits_{x\rightarrow0^+}\dfrac{-2.x^2.e^{2x}}{e^{2x}-1}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{2x}{e^{2x}-1}.\left(-x.e^{2x}\right)=1.\left(-0.1\right)=0\)
c.
Do \(-1\le cos\left(x^2\right)\le-1\) \(\Rightarrow-\dfrac{1}{x^2}\le\dfrac{1}{x^2}.cos\left(x^2\right)\le\dfrac{1}{x^2}\)
Mà \(\lim\limits_{x\rightarrow+\infty}\left(-\dfrac{1}{x^2}\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{x^2}\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}\dfrac{1}{x^2}cos\left(x^2\right)=0\)
d.
\(\lim\limits_{x\rightarrow0}\left(\dfrac{x+e^x-1}{x}\right)=\lim\limits_{x\rightarrow0}\left(1+\dfrac{e^x-1}{x}\right)=1+1=2\)
e.
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+1}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{1}{x+\sqrt{x^2+1}}=0\)
f.
\(\lim\limits_{x\rightarrow+\infty}\dfrac{5^{x+2}+7^{x+5}}{6^x+7^x}=\lim\limits_{x\rightarrow+\infty}\dfrac{5^2.\left(\dfrac{5}{7}\right)^x+7^5}{\left(\dfrac{6}{7}\right)^x+1}=\dfrac{25.0+7^5}{0+1}=7^5\)