a) Ta thấy: $(x+2)^2\ge0\forall x$
$\Rightarrow (x+2)^2+5\ge5\forall x$
$\Rightarrow Q\ge5\forall x$
Dấu "=" xảy ra khi: $x+2=0\Rightarrow x=-2$
Vậy $Q_{min}=5$ tại $x=-2$.
b) Ta thấy: $(3x-1)^2\ge0\forall x$
$\Rightarrow (3x-1)^2-4\ge-4\forall x$
$\Rightarrow R\ge-4\forall x$
Dấu "=" xảy ra khi: $3x-1=0\Rightarrow x=\frac13$
Vậy $R_{min}=-4$ tain $x=\frac13$
#$\mathtt{Toru}$
a, \(Q=\left(x+2\right)^2+5\)
Vì \(\left(x+2\right)^2\ge0\\ \Rightarrow\left(x+2\right)^2+5\ge5\\ \Leftrightarrow Q\ge5\)
Dấu " = " xảy ra khi \(\left(x+2\right)^2=0\\ \Leftrightarrow x+2=0\\ \Leftrightarrow x=-2\)
\(\Rightarrow\) Giá trị nhỏ nhất của Q = 5 khi x= -2
b, \(R=\left(3x-1\right)^2-4\)
Vì \(\left(3x-1\right)^2\ge0\\ \Leftrightarrow\left(3x-1\right)^2-4\ge-4\\ \Leftrightarrow R\ge-4\)
Dấu " = " xảy ra khi \(\left(3x-1\right)^2=0\\ \Leftrightarrow3x-1=0\\ \Rightarrow x=\dfrac{1}{3}\)
\(\Rightarrow\) Giá trị nhỏ nhất của R = -4 khi \(x=\dfrac{1}{3}\)

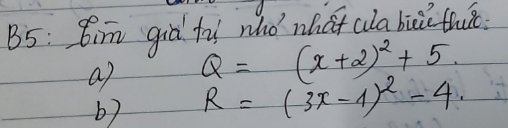























 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước