(a) \(P\left(x\right)=2x^3-2x+x^2+3x+2\)
\(=2x^3+x^2+\left(3x-2x\right)+2\)
\(=2x^3+x^2+x+2.\)
\(Q\left(x\right)=4x^3-3x^2-3x+4x-3x^3+4x^2+1\)
\(=\left(4x^3-3x^3\right)+\left(4x^2-3x^2\right)+\left(4x-3x\right)+1\)
\(=x^3+x^2+x+1\)
(b) Thay \(x=-1\) vào \(P\left(x\right)\), ta được:
\(P\left(-1\right)=2\left(-1\right)^3+\left(-1\right)^2+\left(-1\right)+2=0\)
Vậy: \(x=-1\) là một nghiệm của \(P\left(x\right)\)

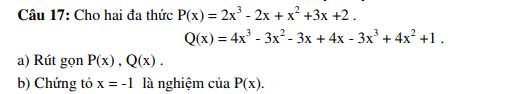





















 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước