Lời giải:
a. Lấy $x_1\neq x_2\in\mathbb{R}$.
Xét \(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{(2x_1+3)-(2x_2+3)}{x_1-x_2}=\frac{2(x_1-x_2)}{x_1-x_2}=2>0, \forall x_1\neq x_2\in\mathbb{R}\)
Do đó hàm đồng biến trên $\mathbb{R}$
b. Lấy $x_1\neq x_2\in (-\infty; -5)$
Xét \(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{(x_1^2+10x_1+9)-(x_2^2+10x_2+9)}{x_1-x_2}=\frac{(x_1-x_2)(x_1+x_2+10)}{x_1-x_2}\)
$=x_1+x_2+10< 0$ với mọi $(-\infty; -5)$
Do đó hàm nghịch biến trên $(-\infty; -5)$. Xét tương tự thì hàm đồng biến trên $(-5;+\infty)$
c. Lấy $x_1\neq x_2\in (-\infty; -1)\cup (-1;+\infty)$
Xét \(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\frac{4}{x_1+1}-\frac{4}{x_2+1}}{x_1-x_2}=\frac{-4}{(x_1+1)(x_2+1)}<0\) với mọi $x_1\neq x_2\in (-\infty; -1)\cup (-1;+\infty)$
Vậy hàm số nghịch biến trên $(-\infty;-1)$ và $(-1;+\infty)$









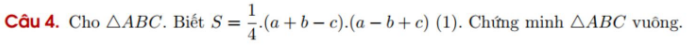






 giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn
giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn




