Phương trình hoành độ giao điểm là:
\(x^2=\left(m+1\right)x-m+5\)
=>\(x^2-x\left(m+1\right)+m-5=0\)
\(\Delta=\left(m+1\right)^2-4\left(m-5\right)=m^2+2m+1-4m+20\)
\(=m^2-2m+21=m^2-2m+1+20=\left(m-1\right)^2+20\ge20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có: \(\begin{cases}x_1+x_2=-\frac{b}{a}=m+1\\ x_1x_2=\frac{c}{a}=m-5\end{cases}\)
Để x1 và x2 đều nguyên thì Δ là số chính phương
=>\(\left(m-1\right)^2+20\) là số chính phương
=>\(m^2-2m+21=k^2\) (k∈Z)
=>\(\left(m-1\right)^2+20-k^2=0\)
=>\(\left(m-1\right)^2-k^2=-20\)
=>(m-1-k)(m-1+k)=-20
=>(m-1-k;m-1+k)∈{(1;-20);(-20;1);(-1;20);(20;-1);(2;-10);(-10;2);(-2;10);(10;-2);(4;-5);(-5;4);(-4;5);(5;-4)]
TH1: m-1-k=1 và m-1+k=-20
=>m-1-k+m-1+k=-20+1=-19
=>2m-2=-19
=>2m=-17
=>\(m=-\frac{17}{2}\) (loại)
TH2: m-1-k=-20 và m-1+k=1
=>m-1-k+m-1+k=-20+1=-19
=>2m-2=-19
=>2m=-17
=>\(m=-\frac{17}{2}\) (loại)
TH3: m-1-k=-1 và m-1+k=20
=>m-1-k+m-1+k=-1+20
=>2m-2=19
=>2m=21
=>\(m=\frac{21}{2}\) (loại)
TH4: m-1-k=20 và m-1+k=-1
=>m-1-k+m-1+k=-1+20
=>2m-2=19
=>2m=21
=>\(m=\frac{21}{2}\) (loại)
TH5: m-1-k=2 và m-1+k=-10
=>m-1-k+m-1+k=2-10=-8
=>2m-2=-8
=>2m=-6
=>m=-3(nhận)
TH6: m-1-k=-10 và m-1+k=2
=>m-1-k+m-1+k=2-10=-8
=>2m-2=-8
=>2m=-6
=>m=-3(nhận)
TH7: m-1-k=-2 và m-1+k=10
=>m-1-k+m-1+k=-2+10
=>2m-2=8
=>2m=10
=>m=5(nhận)
TH8: m-1-k=10 và m-1+k=-2
=>m-1-k+m-1+k=-2+10
=>2m-2=8
=>2m=10
=>m=5(nhận)
TH9: m-1-k=4 và m-1+k=-5
=>m-1-k+m-1+k=4-5
=>2m-2=-1
=>2m=1
=>\(m=\frac12\) (loại)
TH10: m-1-k=-5 và m-1+k=4
=>m-1-k+m-1+k=4-5
=>2m-2=-1
=>2m=1
=>\(m=\frac12\) (loại)
TH11: m-1-k=-4 và m-1+k=5
=>m-1-k+m-1+k=-4+5
=>2m-2=1
=>2m=3
=>\(m=\frac32\) (loại)
TH12: m-1-k=5 và m-1+k=-4
=>m-1-k+m-1+k=-4+5
=>2m-2=1
=>2m=3
=>\(m=\frac32\) (loại)
Vậy: m∈{5;-3}











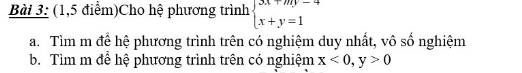 Giúp mình với mai kt rôi mà mình ko biết làm câu b?
Giúp mình với mai kt rôi mà mình ko biết làm câu b?