a: \(A=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right)\cdot\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{-4x^2-8x}{\left(x+2\right)}\cdot\dfrac{-x}{x-3}=\dfrac{4x^2\left(x+2\right)}{\left(x+2\right)\left(x-3\right)}=\dfrac{4x^2}{x-3}\)
b: Để A chia hết cho 4 thì x^2/x-3 chia hết cho 4 và x^2 chia hết cho x-3
=>x^2/x-3=4k(k thuộc Z) và x^2-9+9 chia hết cho x-3
=>\(x-3\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(x\in\left\{4;2;6;0;12;-6\right\}\)
Kết hợp ĐK chia hết cho 4, ta được: \(x\in\left\{4;12;-6\right\}\)

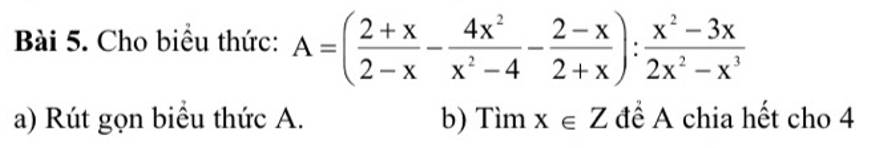







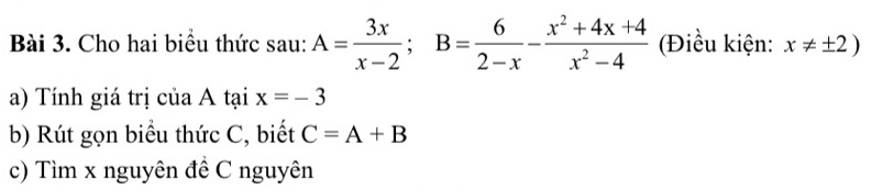















 Giúp mình với ạ!! Cảm ơn nhiều
Giúp mình với ạ!! Cảm ơn nhiều