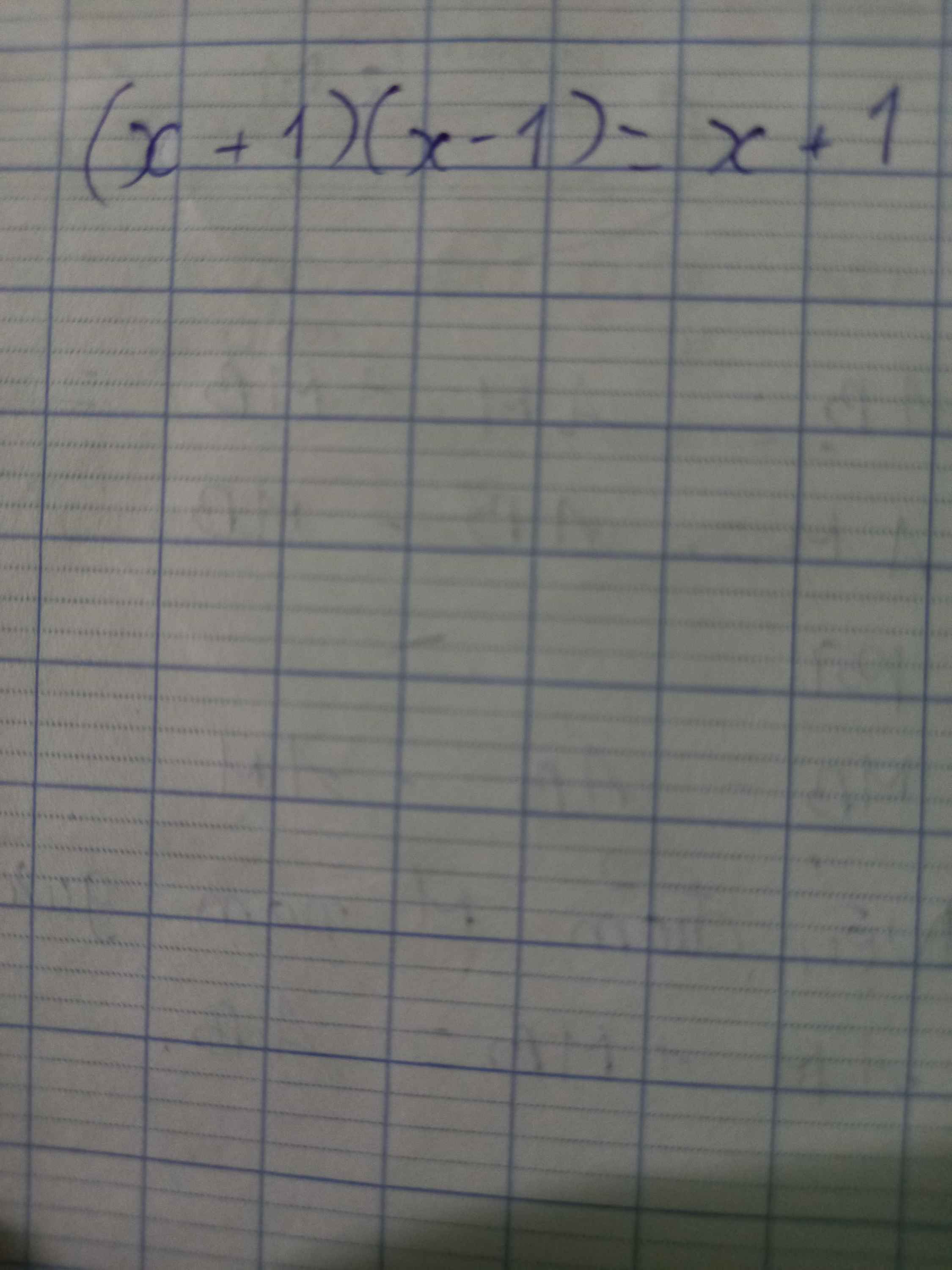\(1,\left(x+2\right)\left(3x-4\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+2=0\\3x-4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)
\(2,\dfrac{x-51}{9}+\dfrac{x-52}{8}=\dfrac{x-53}{7}+\dfrac{x-54}{6}\\ \Leftrightarrow\left(\dfrac{x-51}{9}-1\right)+\left(\dfrac{x-52}{8}-1\right)=\left(\dfrac{x-53}{7}-1\right)+\left(\dfrac{x-54}{6}-1\right)\\ \Leftrightarrow\dfrac{x-60}{9}+\dfrac{x-60}{8}-\dfrac{x-60}{7}-\dfrac{x-60}{6}=0\\ \Leftrightarrow\left(x-60\right)\left(\dfrac{1}{9}+\dfrac{1}{8}-\dfrac{1}{7}-\dfrac{1}{6}\right)=0\)
Vì \(\dfrac{1}{9}+\dfrac{1}{8}-\dfrac{1}{7}-\dfrac{1}{6}\ne0\Rightarrow x-60=0\Rightarrow x=60\)
3,ĐKXĐ:\(x\ne\pm2\)
\(\dfrac{x-2}{x+2}+\dfrac{3}{x-2}=\dfrac{x^2-11}{x^2-4}\\ \Leftrightarrow\left(x-2\right)^2+3\left(x+2\right)=x^2-11\\ \Leftrightarrow x^2-4x+4+3x+6-x^2+11=0\)
\(\Leftrightarrow-x+21=0\\ \Leftrightarrow-x=-21\\ \Leftrightarrow x=21\left(tm\right)\)
\(4,\dfrac{x^2+1}{2}=\dfrac{2x^2+x}{3}\\ \Leftrightarrow3\left(x^2+1\right)=2\left(2x^2+x\right)\\ \Leftrightarrow3x^2+3=4x^2+2x\\ \Leftrightarrow4x^2+2x-3x^2-3=0\\ \Leftrightarrow x^2+2x-3=0\\ \Leftrightarrow\left(x^2+3x\right)-\left(x+3\right)=0\\ \Leftrightarrow x\left(x+3\right)-\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
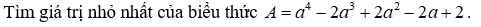
giúp mình với ạ mình cảm ơn
