a: \(P=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-2\sqrt{x}-1\)
\(=\sqrt{x}\left(\sqrt{x}+1\right)-2\sqrt{x}=x-\sqrt{x}\)
b: \(P=x-\sqrt{x}\)
\(=x-\sqrt{x}+\dfrac{1}{4}-\dfrac{1}{4}\)
\(=\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}>=-\dfrac{1}{4}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{1}{2}=0\)
=>\(\sqrt{x}=\dfrac{1}{2}\)
=>x=1/4(nhận)


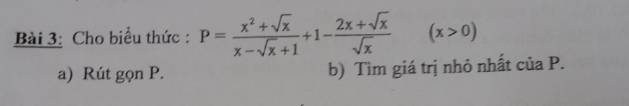 Gi
Gi



 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn






