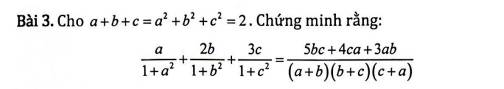Question

Giúp mình giải bài này với mọi người.

Answer 1

Lời giải:

\(ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-2}{2}=1\)

Khi đó:

\(\text{VT}=\frac{a}{ab+bc+ac+a^2}+\frac{2b}{ab+bc+ac+b^2}+\frac{3c}{ab+bc+ac+c^2}\)

\(=\frac{a}{(a+b)(a+c)}+\frac{2b}{(b+a)(b+c)}+\frac{3c}{(c+a)(c+b)}\)

\(=\frac{a(b+c)+2b(a+c)+3c(a+b)}{(a+b)(b+c)(c+a)}\)

\(=\frac{3ab+4ac+5bc}{(a+b)(b+c)(c+a)}=\text{VP}\)