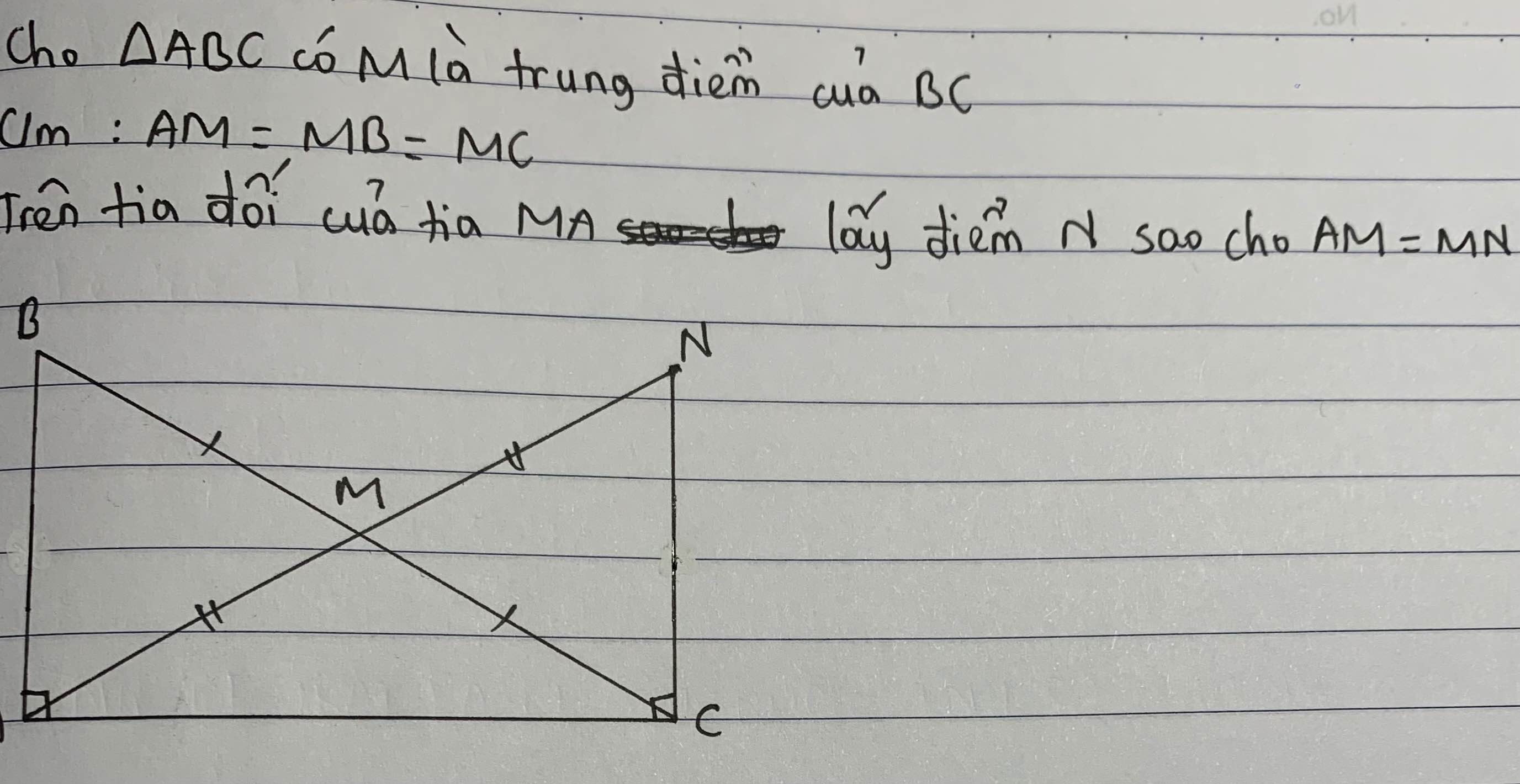
Trên tia đối của tia MA, lấy N sao cho MA=MN
Xét ΔMAB và ΔMNC có
MA=MN
\(\widehat{AMB}=\widehat{NMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMNC
=>\(\widehat{MAB}=\widehat{MNC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//NC
Ta có: AB//NC
AB\(\perp\)AC
Do đó: CN\(\perp\)CA
Xét ΔBAC vuông tại A và ΔNCA vuông tại C có
BA=NC
AC chung
Do đó: ΔBAC=ΔNCA
=>BC=NA
mà \(MA=\dfrac{NA}{2};MB=MC=\dfrac{BC}{2}\)
nên MA=MB=MC
Đúng 1
Bình luận (0)
