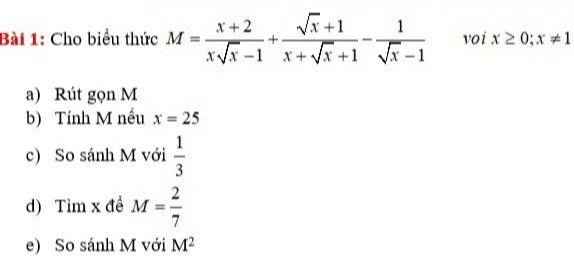`a)M=(x+2)/(xsqrtx-1)+(sqrtx+1)/(x+sqrtx+1)-1/(sqrtx-1)(x>=0,x ne 1)`
`M=(x+2)/((sqrtx-1)(x+sqrtx+1))+((sqrtx+1)(sqrtx-1))/((sqrtx-1)(x+sqrtx+1))-(x+sqrtx+1)/((sqrtx-1)(x+sqrtx+1))`
`M=(x+2+x-1-x-sqrtx-1)/((sqrtx-1)(x+sqrtx+1))`
`M=(x-sqrtx)/((sqrtx-1)(x+sqrtx+1))`
`M=(sqrtx(sqrtx-1))/((sqrtx-1)(x+sqrtx+1))`
`M=sqrtx/(x+sqrtx+1)`
`b)x=25(tmđk)`
`=>sqrtx=5`
`=>M=5/(25+5+1)`
`=>M=5/31`
`c)M=sqrtx/(x+sqrtx+1)`
`x=0=>M=0<1/3`
`x>0=>M=1/(sqrtx+1+1/sqrtx)`
Áp dụng bđt cosi:
`sqrtx+1/sqrtx>=2`
`=>sqrtx+1+1/sqrtx>=3>0`
`=>M<=1/3`
Dấu "=" xảy ra khi `sqrtx=1/sqrtx<=>x=1`(KTMĐKXĐ)
`=>M<1/3`
Vậy `M<1/3`
`d)M=2/7`
`<=>sqrtx/(x+sqrtx+1)=2/7`
`<=>2x+2sqrtx+2=7`
`<=>2x-5sqrtx+2=0`
`<=>2x-4sqrtx-sqrtx+2=0`
`<=>(sqrtx-2)(2sqrtx-1)=0`
`<=>[(sqrtx=2),(2sqrtx=1):}`
`<=>[(x=4),(x=1/4):}(TMĐK)`
`e)` Vì `x>=0=>sqrtx>=0`
`=>x+sqrtx+1>=1>0`
`=>M>=0`
Mặt khác:`M<1/3`(câu b)
`=>M<1=>M-1<0`
`=>M(M-1)<=0`
`<=>M^2-M<=0`
`<=>M^2<=M`
a: Ta có: \(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
b: Thay x=25 vào M, ta được:
\(M=\dfrac{5}{25+5+1}=\dfrac{5}{31}\)
c: Ta có: \(M-\dfrac{1}{3}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)
\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(x-2\sqrt{x}+1\right)}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}-1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\forall x\) thỏa mãn ĐKXĐ
hay \(M< \dfrac{1}{3}\)
d: Để \(M=\dfrac{2}{7}\) thì \(2x+2\sqrt{x}+2=7\sqrt{x}\)
\(\Leftrightarrow2x-5\sqrt{x}+2=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=\dfrac{1}{4}\left(nhận\right)\end{matrix}\right.\)