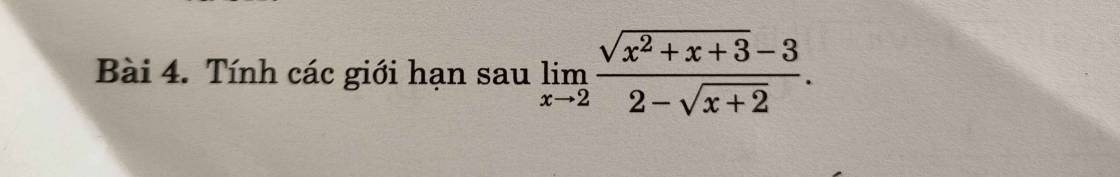Lời giải:
\(\lim\limits_{x\to 2}\frac{\sqrt{x^2+x+3}-3}{2-\sqrt{x+2}}=\lim\limits_{x\to 2}\frac{\frac{x^2+x+3-9}{\sqrt{x^2+x+3}+3}}{\frac{4-(x+2)}{2+\sqrt{x+2}}}=\lim\limits_{x\to 2}\frac{x^2+x-6}{2-x}.\frac{2+\sqrt{x+2}}{\sqrt{x^2+x+3}+3}\)
\(=\lim\limits_{x\to 2}\frac{(x-2)(x+3)}{2-x}.\frac{2+\sqrt{x+2}}{\sqrt{x^2+x+3}+3}=\lim\limits_{x\to 2}-(x+3).\frac{2+\sqrt{x+2}}{\sqrt{x^2+x+3}+3}=\frac{-10}{3}\)
Đúng 1
Bình luận (0)