\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân.tại.A\right)\\\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân.tại.A\right)\\AD.chung\end{matrix}\right.\Rightarrow\Delta ADB=\Delta ADC\left(ch-gn\right)\)
\(b,\)Áp dụng định lí Py-ta-go cho tam giác ABD vuông tại D
\(AD^2=AB^2-BD^2=36\\ \Rightarrow AD=6\left(cm\right)\)
\(c,\) Vì tam giác BAC cân tại A nên đường cao AD cũng là trung tuyến
Mà G là trọng tâm nên \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot6=4\left(cm\right)\)







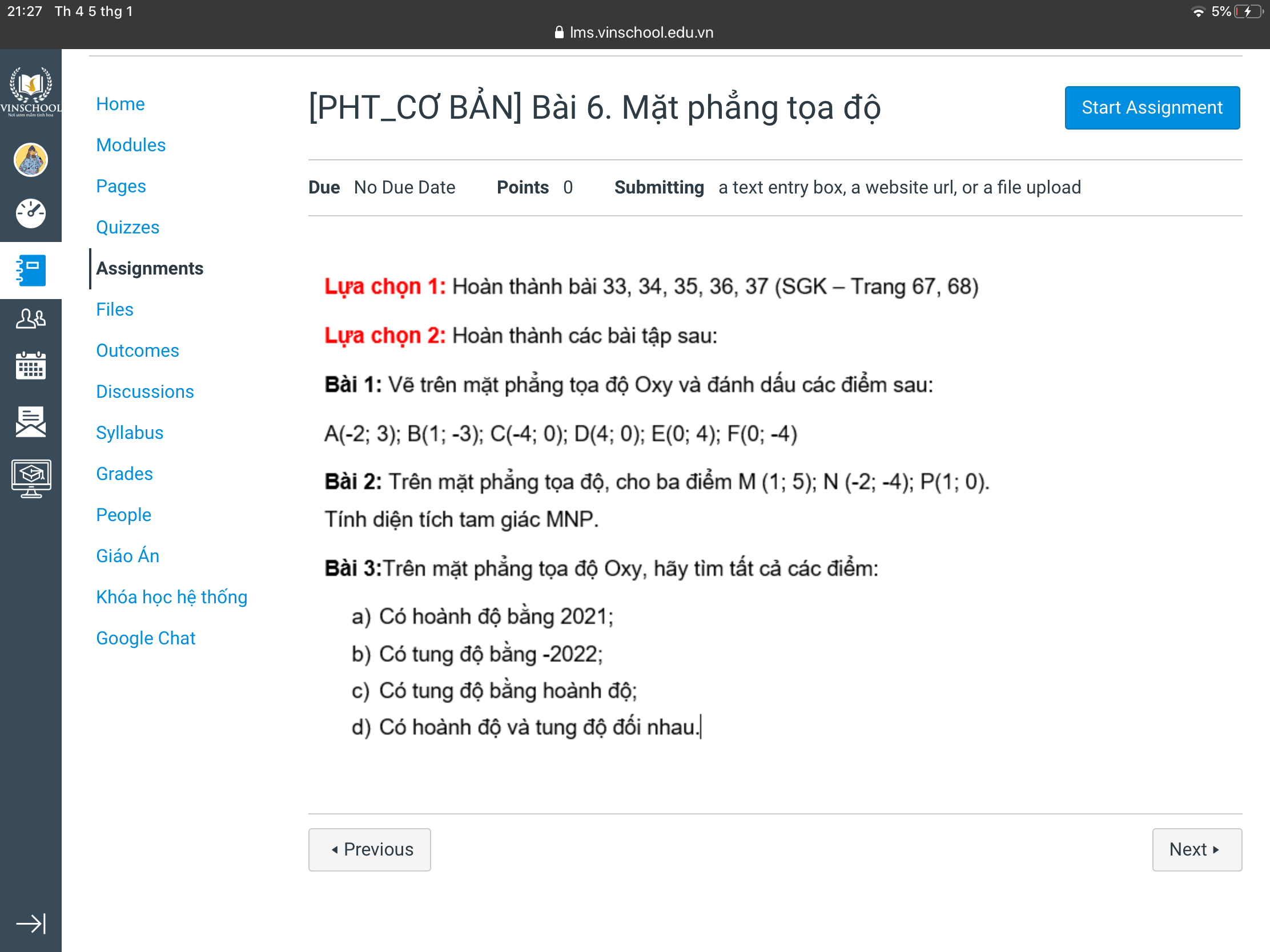 Làm giúp e câu 3 với ạ🥺
Làm giúp e câu 3 với ạ🥺



 mn giúp mình câu c và d thôi ạ
mn giúp mình câu c và d thôi ạ