\(a,tan\alpha=\dfrac{1}{3}\Rightarrow\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{3}\\ \Rightarrow cos\alpha=3sin\alpha\\Mà:sin^2\alpha+cos^2\alpha=1\\ \Leftrightarrow sin^2\alpha+\left(3sin\alpha\right)^2=1\\ \Leftrightarrow10sin^2\alpha=1\\ \Leftrightarrow sin^2\alpha=\dfrac{1}{10}\\ \Rightarrow sin\alpha=\sqrt{\dfrac{1}{10}}\approx0,3162\\ cos\alpha=\sqrt{1-\dfrac{1}{10}}=\sqrt{\dfrac{9}{10}}\approx0,9487\)
\(b,cot\alpha=\dfrac{3}{4}\Rightarrow\dfrac{cos\alpha}{sin\alpha}=\dfrac{3}{4}\Leftrightarrow cos\alpha=\dfrac{3}{4}sin\alpha\\ Ta.có:cos^2\alpha+sin^2\alpha=1\\ \Leftrightarrow\left(\dfrac{3}{4}sin\alpha\right)^2+sin^2\alpha=1\\ \Leftrightarrow\dfrac{9}{16}sin^2\alpha+sin^2\alpha=1\\ \Leftrightarrow\dfrac{25}{16}sin^2\alpha=1\\ \Leftrightarrow sin^2\alpha=1:\dfrac{25}{16}=\dfrac{16}{25}\\ \Rightarrow sin\alpha=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}\\ Vậy:cos\alpha=\sqrt{1-\dfrac{16}{25}}=\sqrt{\dfrac{9}{25}}=\dfrac{3}{5}\)











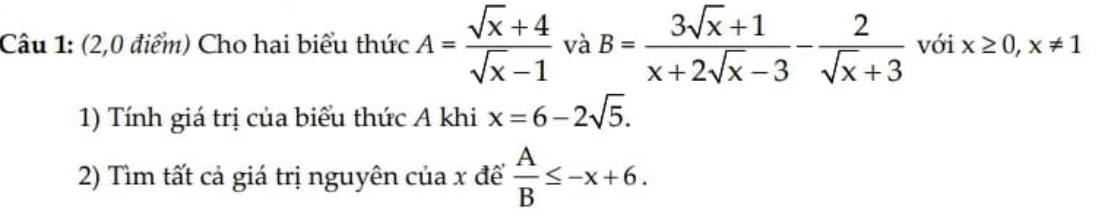
 giúp mình câu b với ạ
giúp mình câu b với ạ



 giúp mình câu a, b với ạ
giúp mình câu a, b với ạ
