a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC
b: Xét ΔOBA vuông tại B có
\(\sin BAC=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAC}=30^0\)















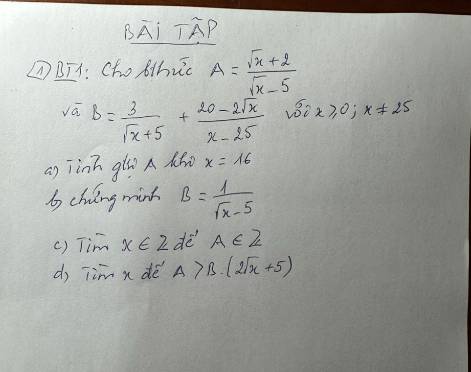


 giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với


 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!