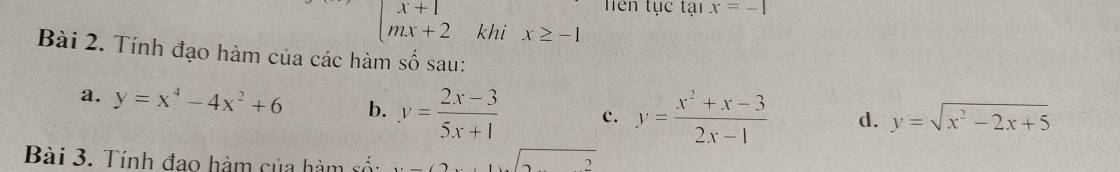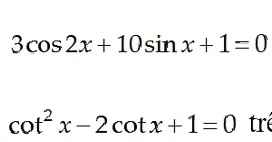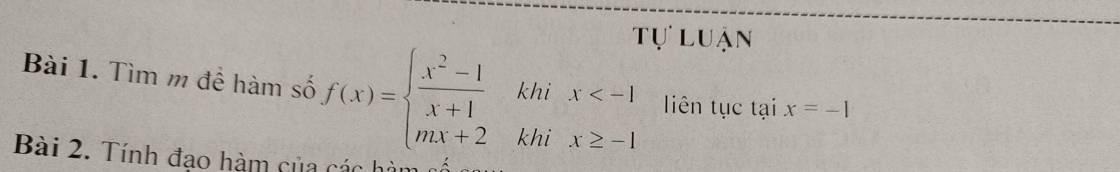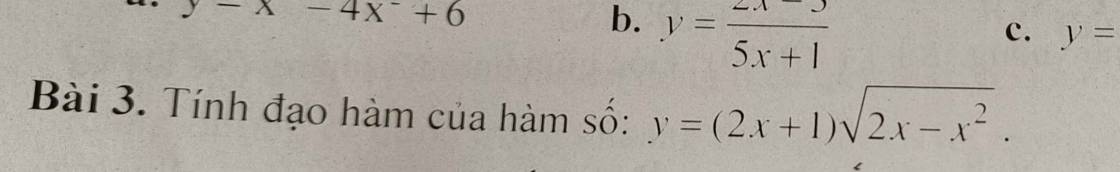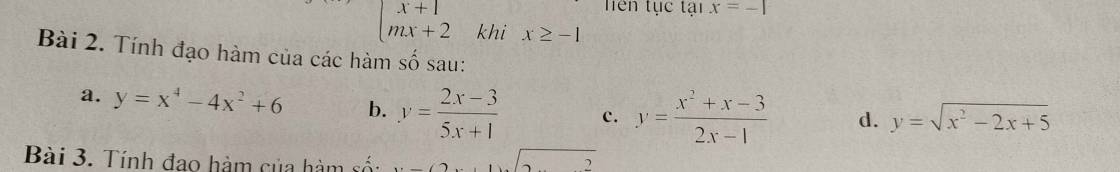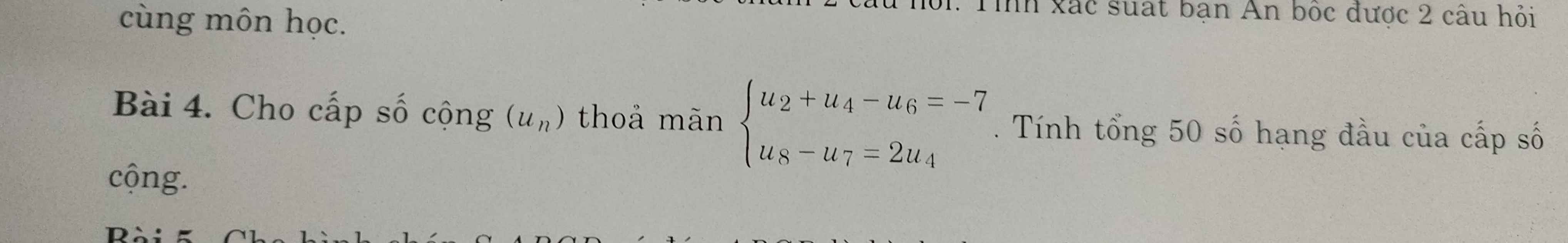4:
a: BD vuông góc SA
BD vuông góc AC
=>BD vuông góc (SAC)
b: SA=3a; AB=BC=CD=DA=a
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{11}\)
\(SB=\sqrt{\left(3a\right)^2+a^2}=a\sqrt{10}\)
\(SD=\sqrt{9a^2+a^2}=a\sqrt{10}\)
SB^2+BC^2=SC^2
=>ΔSBC vuông tại B
\(cosDSB=\dfrac{10a^2+10a^2-2a^2}{2\cdot10a^2}=\dfrac{9}{10}\)
vecto SB*vecto CD
=vecto SB*vecto SD-vecto SB*vecto SC
=\(SB\cdot SD\cdot\dfrac{9}{10}-SB\cdot SC\cdot cosBSC\)
\(=a\sqrt{10}\cdot a\sqrt{10}\cdot\dfrac{9}{10}-a\sqrt{10}\cdot a\sqrt{11}\cdot\dfrac{a\sqrt{10}}{a\sqrt{11}}\)
\(=-a^2\)
=>\(cos\left(SB;CD\right)=\left|\dfrac{-a^2}{SB\cdot CD}\right|=\left|\dfrac{-a^2}{a\sqrt{10}\cdot a}\right|=\dfrac{\sqrt{10}}{10}\)
=>\(sin\left(SB;CD\right)=\dfrac{3\sqrt{10}}{10}\)