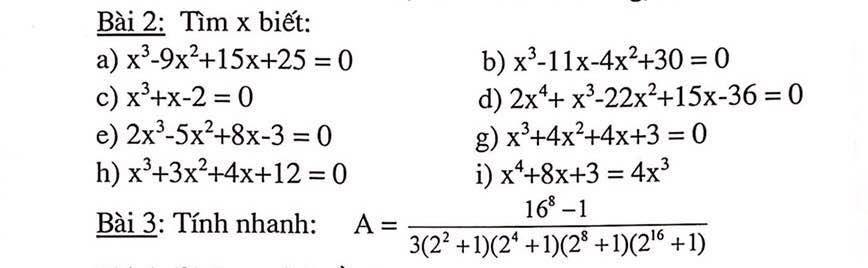h: Ta có: \(x^3+3x^2+4x+12=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3
A = \(\dfrac{16^8-1}{3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{\left(2^4\right)^8-1}{\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^{16}-1\right)\left(2^{16}+1\right)}=\dfrac{2^{32}-1}{2^{32}-1}=1\)