\(x^2-2\left(m-2\right)x+3-2m=0\left(1\right)\)
a. \(\Delta'=\left(m-2\right)^2-\left(3-2m\right)=m^2-2m+1=\left(m-1\right)^2\ge0\)
=> (1) luôn có nghiệm với mọi giá trị của m
b. Theo Viet \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=3-2m\end{matrix}\right.\)
Theo bài ra \(\left|x_1-x_2\right|=24\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=576\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=576\)
\(\Leftrightarrow4\left(m-2\right)^2-4\left(3-2m\right)=576\)
\(\Leftrightarrow4m^2-8m-572=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=13\\m=-11\end{matrix}\right.\)
Vậy m = 13 hoặc m = -11






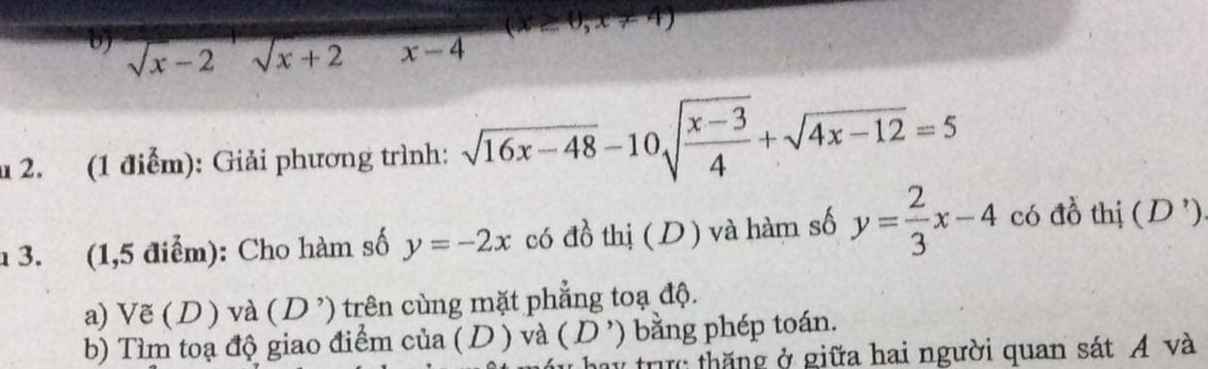











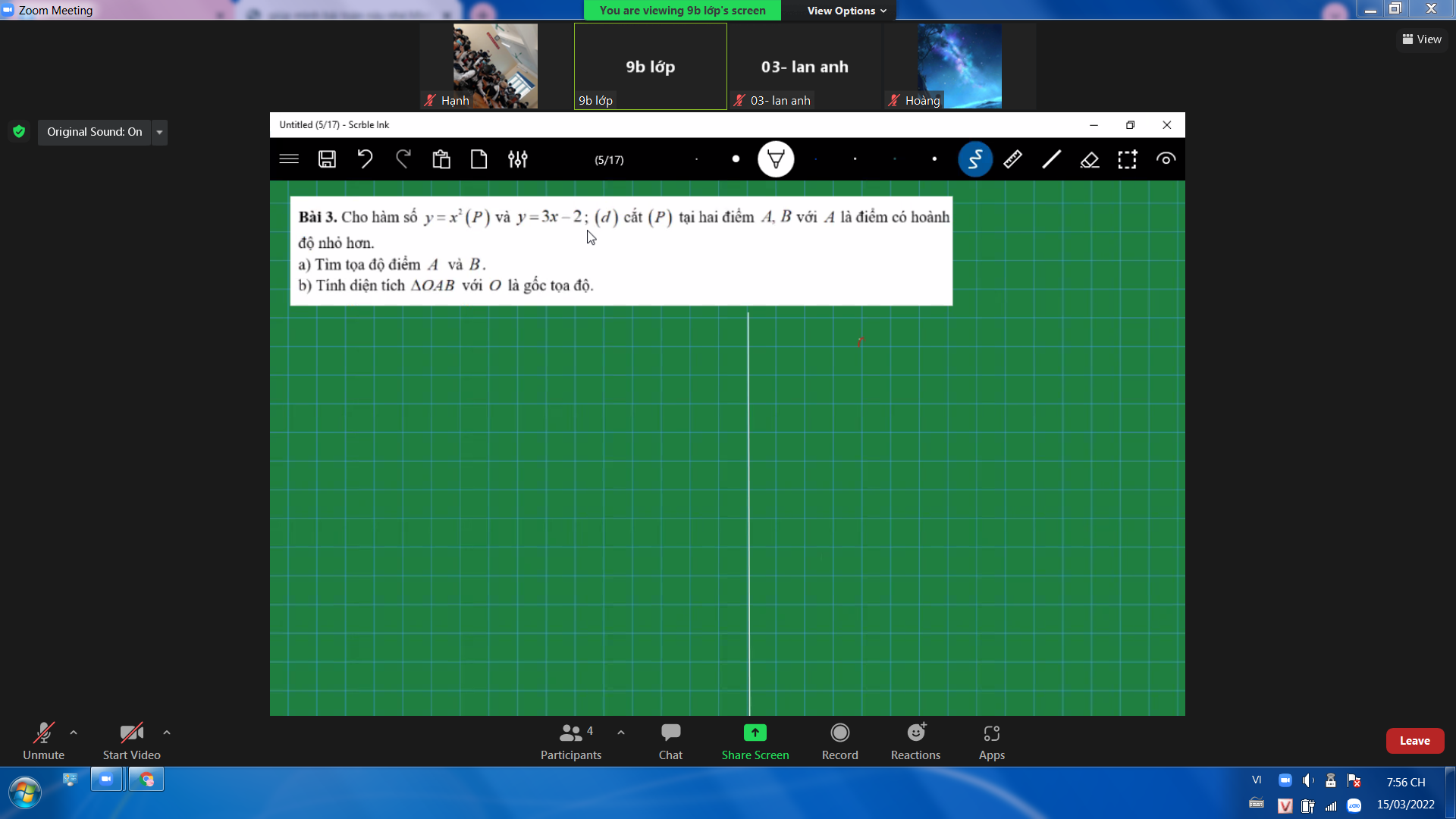
 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ