Bài 1:
e: \(\dfrac{2x-1}{5}-\dfrac{x-2}{3}=\dfrac{x+7}{15}\)
=>\(\dfrac{3\left(2x-1\right)-5\left(x-2\right)}{15}=\dfrac{x+7}{15}\)
=>3(2x-1)-5(x-2)=x+7
=>6x-3-5x+10=x+7
=>x+7-x-7=0
=>0x=0
=>\(x\in R\)
f: \(\dfrac{x-23}{24}+\dfrac{x-23}{25}=\dfrac{x-23}{26}+\dfrac{x-23}{27}\)
=>\(\left(x-23\right)\left(\dfrac{1}{24}+\dfrac{1}{25}-\dfrac{1}{26}-\dfrac{1}{27}\right)=0\)
=>x-23=0
=>x=23
c: \(\left(x-3\right)\left(x+4\right)-2\left(3x-2\right)=\left(x-4\right)^2\)
=>\(x^2+4x-3x-12-6x+4=x^2-8x+16\)
=>-7x-8=-8x+16
=>-7x+8x=16+8
=>x=24
d: \(\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=\dfrac{5}{3}+2x\)
=>\(\dfrac{3\left(3x+2\right)}{6}-\dfrac{3x+1}{6}=\dfrac{10}{6}+\dfrac{12x}{6}\)
=>3(3x+2)-3x-1=10+12x
=>9x+6-3x-1=10+12x
=>12x+10=3x+5
=>9x=-5
=>\(x=-\dfrac{5}{9}\)
a: 5-(x-6)=4(3-2x)
=>12-8x=5-x+6=11-x
=>-8x+x=11-12
=>-7x=-1
=>\(x=\dfrac{1}{7}\)
b: \(3-x\left(1-3x\right)=5\left(1-2x\right)\)
=>\(3-x+3x^2=5-10x\)
=>\(3x^2-x+3-5+10x=0\)
=>\(3x^2+9x-2=0\)
\(\text{Δ}=9^2-4\cdot3\cdot\left(-2\right)=81+24=105>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-9-\sqrt{105}}{2\cdot3}=\dfrac{-9-\sqrt{105}}{6}\\x=\dfrac{-9+\sqrt{105}}{6}\end{matrix}\right.\)
Bài 3:
a: ĐKXĐ: \(x\ne2\)
\(\dfrac{2x+5}{x-2}=-3\)
=>\(-3\left(x-2\right)=2x+5\)
=>-3x+6=2x+5
=>-5x=-1
=>\(x=\dfrac{1}{5}\left(nhận\right)\)
b: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\dfrac{x-5}{x+3}-1=\dfrac{5x-2}{9-x^2}\)
=>\(\dfrac{x-5-x-3}{x+3}=\dfrac{-5x+2}{\left(x-3\right)\left(x+3\right)}\)
=>\(\dfrac{-8}{x+3}=\dfrac{-5x+2}{\left(x-3\right)\left(x+3\right)}\)
=>\(\dfrac{-8\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{-5x+2}{\left(x-3\right)\left(x+3\right)}\)
=>-8x+24=-5x+2
=>-8x+5x=2-24
=>-3x=-22
=>\(x=\dfrac{22}{3}\left(nhận\right)\)
c: ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
\(\dfrac{x}{x+1}+2=\dfrac{2x-3}{x}+\dfrac{3}{x\left(x+1\right)}\)
=>\(\dfrac{x^2}{x\left(x+1\right)}+\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(2x-3\right)}{x}+\dfrac{3}{x\left(x+1\right)}\)
=>\(x^2+2x\left(x+1\right)=\left(x+1\right)\left(2x-3\right)+3\)
=>\(3x^2+2x=2x^2-3x+2x-3+3\)
=>\(3x^2+2x-2x^2+x=0\)
=>\(x^2+3x=0\)
=>x(x+3)=0
=>\(\left[{}\begin{matrix}x=0\left(loại\right)\\x=-3\left(nhận\right)\end{matrix}\right.\)
d: ĐKXĐ: \(x\notin\left\{0;4\right\}\)
\(\dfrac{x+2}{x}-\dfrac{1-x}{4-x}=\dfrac{3x-8}{x^2-4x}\)
=>\(\dfrac{x+2}{x}-\dfrac{x-1}{x-4}=\dfrac{3x-8}{x\left(x-4\right)}\)
=>\(\dfrac{\left(x+2\right)\left(x-4\right)-x\left(x-1\right)}{x\left(x-4\right)}=\dfrac{3x-8}{x\left(x-4\right)}\)
=>(x+2)(x-4)-x(x-1)=3x-8
=>\(x^2-2x-8-x^2+x=3x-8\)
=>3x-8=-x-8
=>4x=0
=>x=0(loại)
e: ĐKXĐ: \(x\notin\left\{5;-5\right\}\)
\(\dfrac{x-2}{x+5}-\dfrac{3}{x-5}=\dfrac{2\left(x-11\right)-19}{x^2-25}\)
=>\(\dfrac{\left(x-2\right)\left(x-5\right)-3\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}=\dfrac{2x-41}{\left(x-5\right)\left(x+5\right)}\)
=>(x-2)(x-5)-3(x+5)=2x-41
=>\(x^2-7x+10-3x-15-2x+41=0\)
=>\(x^2-12x+36=0\)
=>\(\left(x-6\right)^2=0\)
=>x-6=0
=>x=6(nhận)
f: ĐKXĐ: \(x\notin\left\{-1;3\right\}\)
\(\dfrac{x}{2x+2}-\dfrac{2x}{x^2-2x-3}=\dfrac{x}{6-2x}\)
=>\(\dfrac{x}{2\left(x+1\right)}-\dfrac{2x}{\left(x-3\right)\left(x+1\right)}=\dfrac{-x}{2\left(x-3\right)}\)
=>\(\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{4x}{2\left(x-3\right)\left(x+1\right)}=\dfrac{-x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}\)
=>x(x-3)-4x=-x(x+1)
=>\(x^2-3x-4x+x^2+x=0\)
=>\(2x^2-6x=0\)
=>2x(x-3)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)






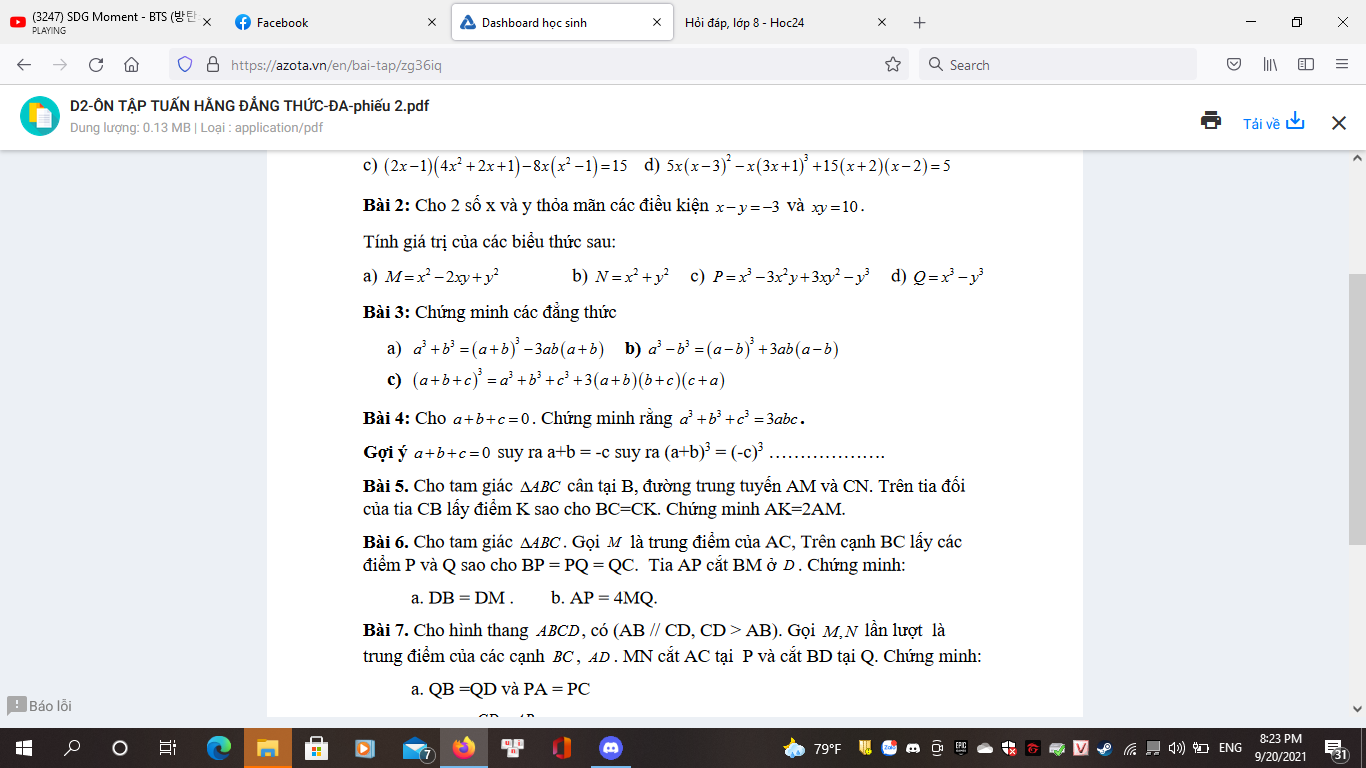 mng giúp mình bài 2 bài 3 bài 4 vs ah
mng giúp mình bài 2 bài 3 bài 4 vs ah


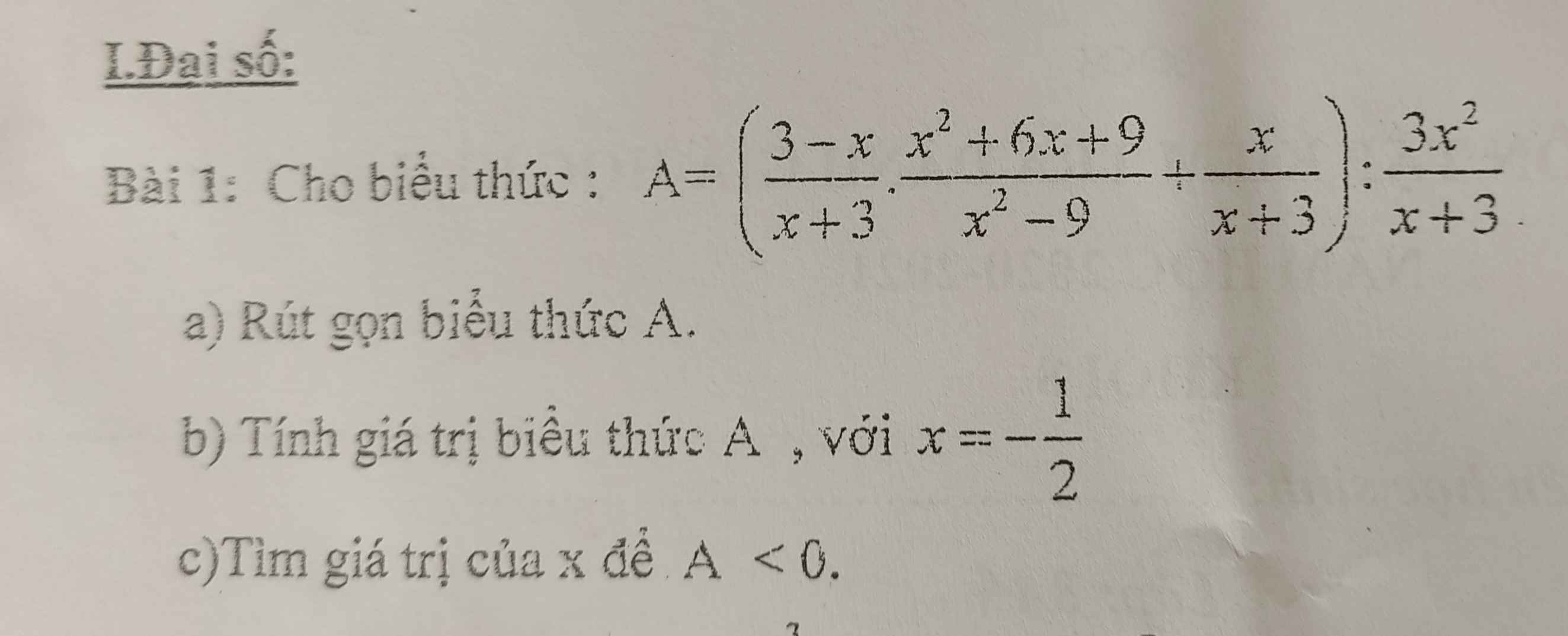










 giúp mình bài 3 vs mn ơi ko phải thi chỉ là đề ôn thôi ạ
giúp mình bài 3 vs mn ơi ko phải thi chỉ là đề ôn thôi ạ