Giúp mình b7,8 nhé :((((((
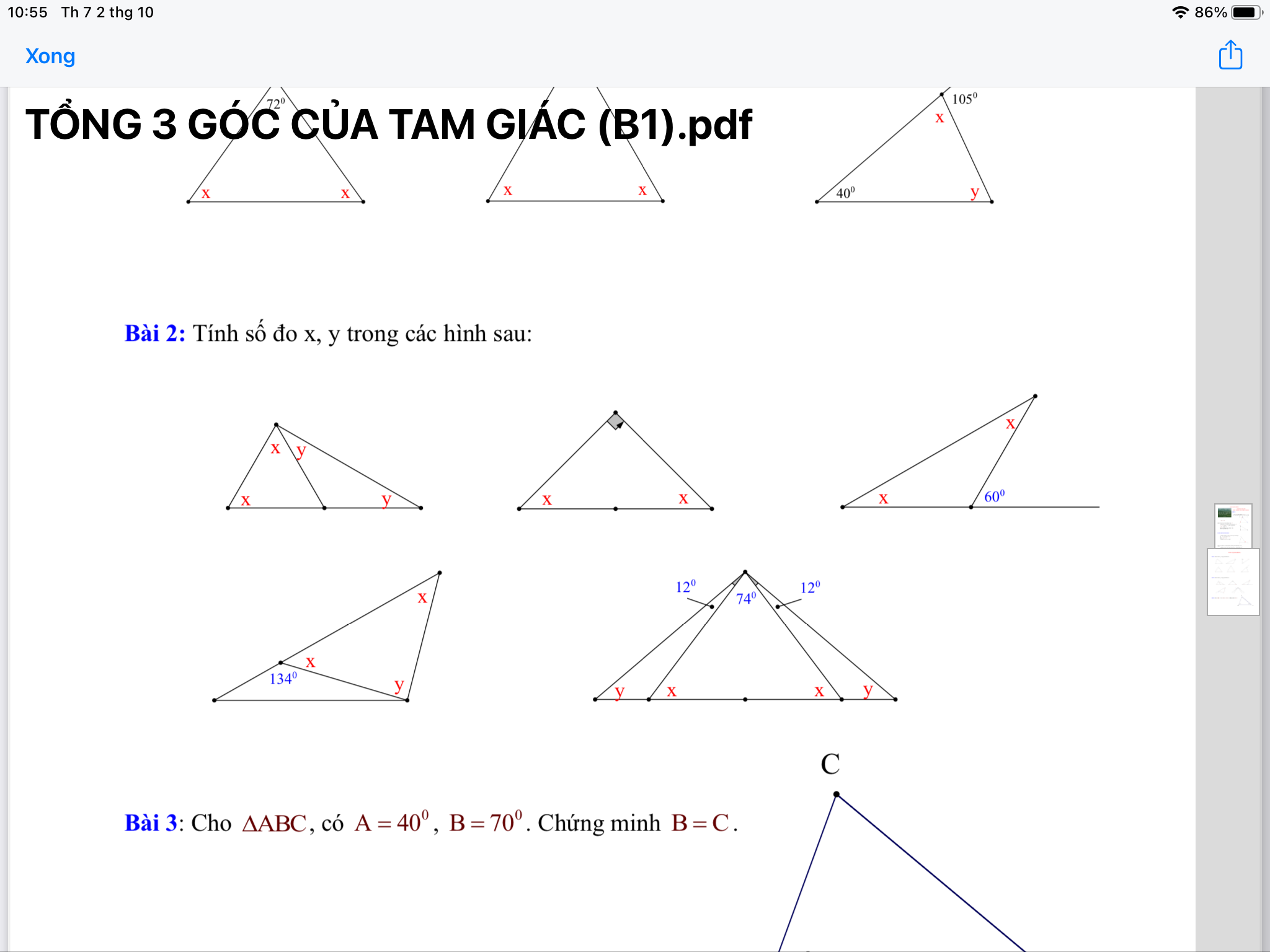
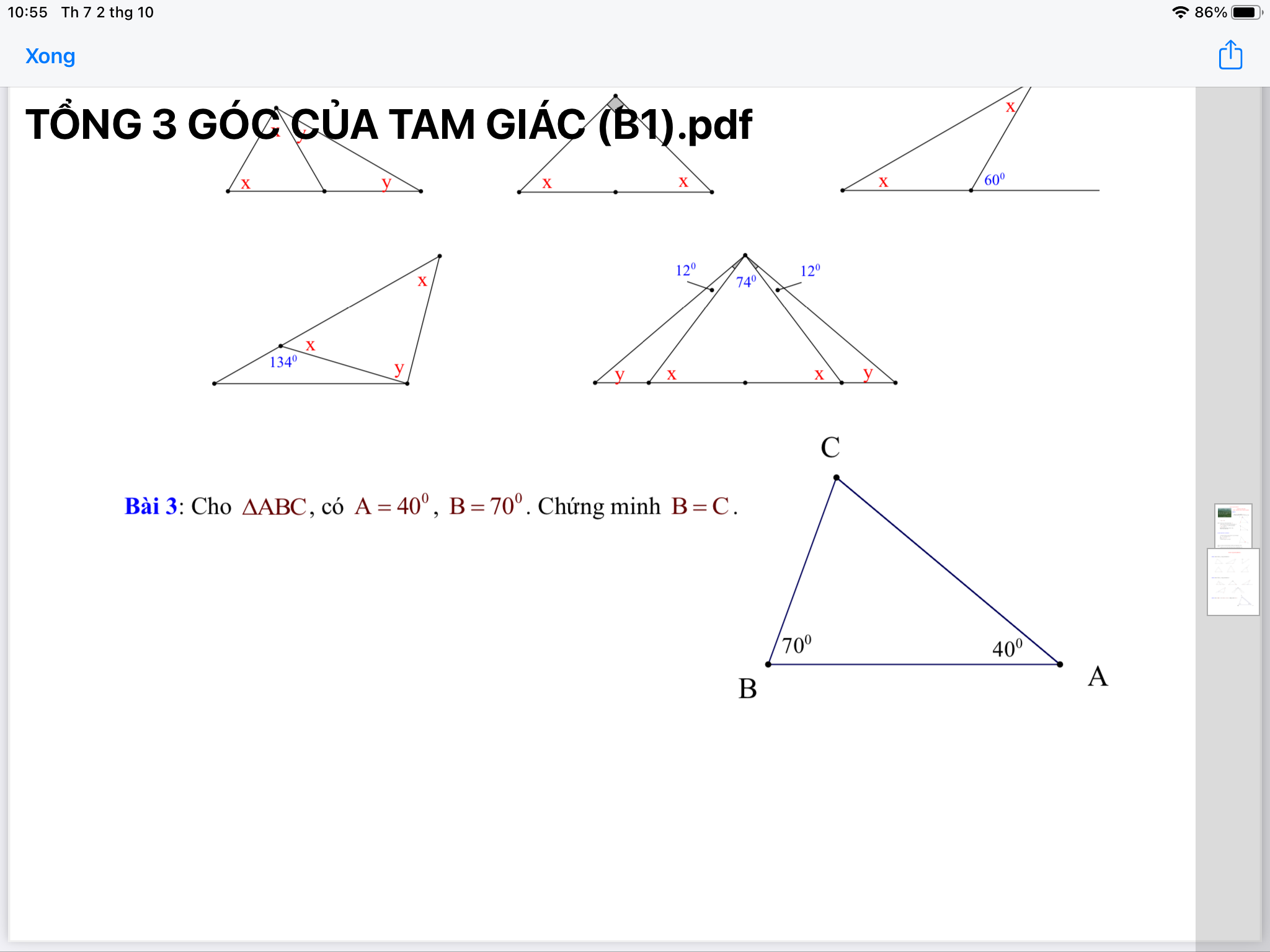
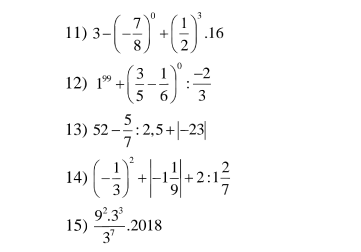Bài 8:
a: ΔCKA vuông tại K
=>\(\widehat{A}+\widehat{C}=90^0\left(1\right)\)
ΔHBC vuông tại H
=>\(\widehat{HBC}+\widehat{C}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{HBC}\)
b: \(\widehat{A}=\widehat{HBC}\)
\(\widehat{HBC}+\widehat{HBK}=180^0\)
Do đó: \(\widehat{A}+\widehat{HBK}=180^0\)
Bài 7:
a: Xét ΔMKN có \(\widehat{MKP}\) là góc ngoài tại đỉnh K
nên \(\widehat{MKP}=\widehat{KMN}+\widehat{KNM}\)
Xét ΔMKP có \(\widehat{MKN}\) là góc ngoài tại đỉnh K
nên \(\widehat{MKN}=\widehat{KMP}+\widehat{KPM}\)
\(\widehat{MKP}-\widehat{MKN}=\widehat{KMN}+\widehat{KNM}-\widehat{KMP}-\widehat{KPM}\)
\(=\widehat{MNP}-\widehat{MPN}\)
