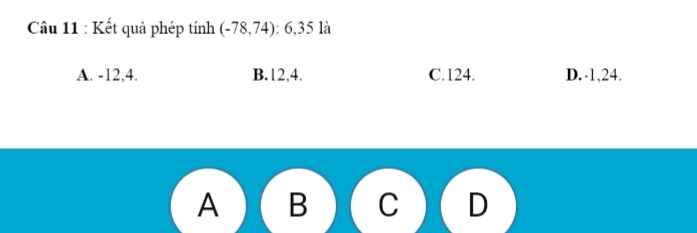
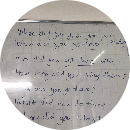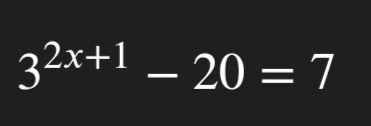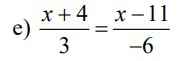a:
Sửa đề: 19/17-19/49+19/131
\(=\dfrac{19\left(\dfrac{1}{17}-\dfrac{1}{49}-\dfrac{1}{131}\right)}{3\left(\dfrac{1}{17}-\dfrac{1}{49}-\dfrac{1}{131}\right)}=\dfrac{19}{3}\)
b: \(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}}{\left(1+\dfrac{2019}{2}\right)+\left(1+\dfrac{2018}{3}\right)+...+\left(1+\dfrac{1}{2020}\right)+1}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}}{2021\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)}=\dfrac{1}{2021}\)
Đúng 0
Bình luận (0)
