\(tana=2\)
=>\(\dfrac{sina}{cosa}=2\)
=>\(sina=2\cdot cosa\)
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=1+2^2=5\)
=>\(cos^2a=\dfrac{1}{5}\)
\(A=sin^2a+2\cdot sina\cdot cosa-3\cdot cos^2a\)
\(=\left(2\cdot cosa\right)^2+2\cdot2\cdot cosa\cdot cosa-3\cdot cos^2a\)
\(=4\cdot cos^2a+4\cdot cos^2a-3\cdot cos^2a=5\cdot cos^2a=5\cdot\dfrac{1}{5}=1\)
\(E=sin^6a+3\cdot sin^2a\cdot cos^2a+cos^6a\)
\(=\left(sin^6a+cos^6a\right)+3\cdot sin^2a\cdot cos^2a\)
\(=\left(sin^2a+cos^2a\right)^3-3\cdot sin^2a\cdot cos^2a\left(sin^2a+cos^2a\right)+3\cdot sin^2a\cdot cos^2a\)
\(=1-3\cdot sin^2a\cdot cos^2a+3\cdot sin^2a\cdot cos^2a\)
=1

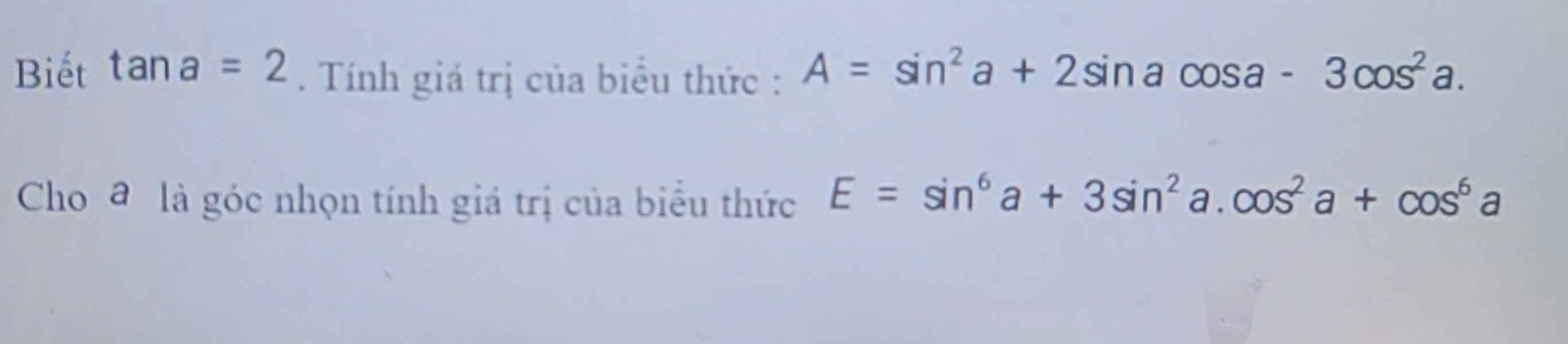




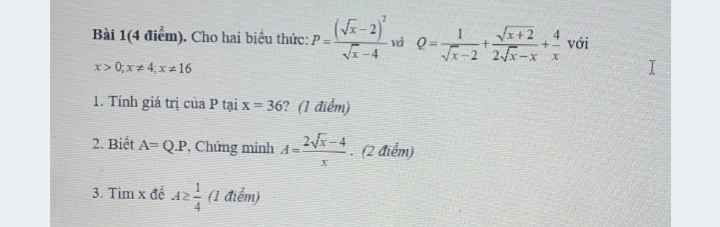





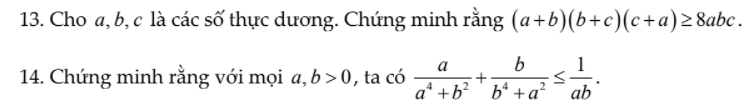

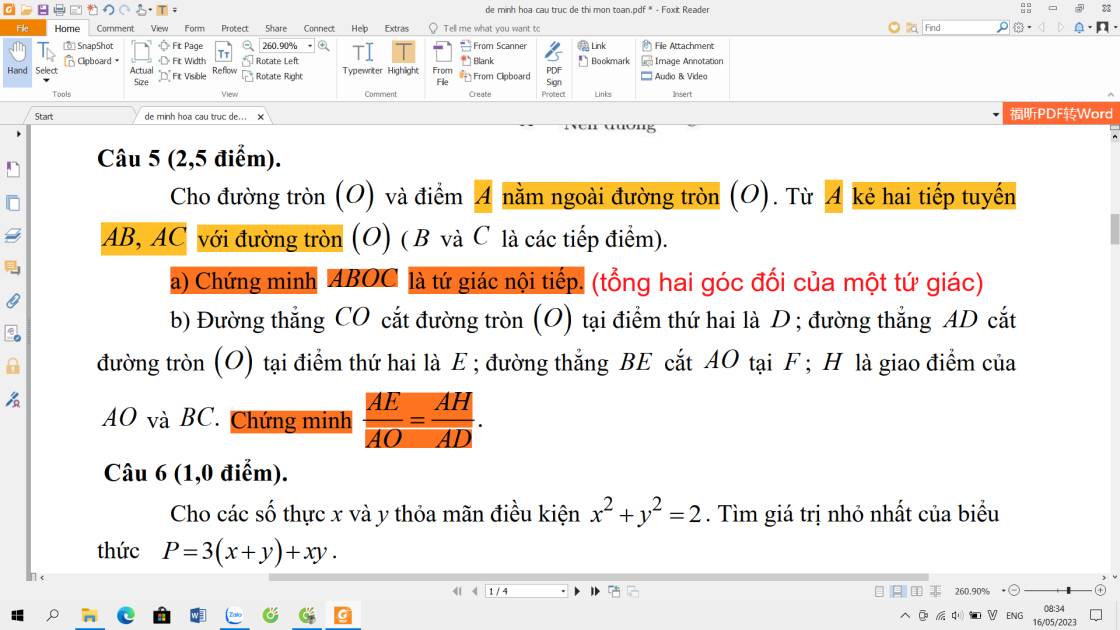 giải giúp mình 2 câu này với ạ
giải giúp mình 2 câu này với ạ








