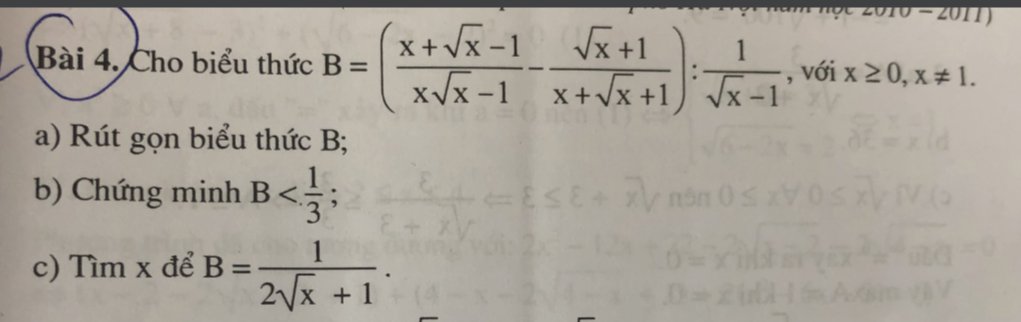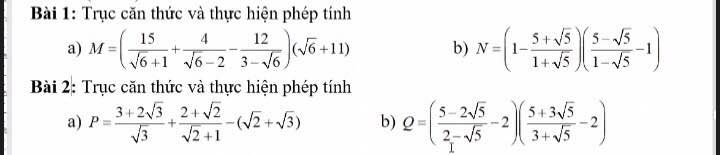Bài 12
- Giả sử \(0^0< \alpha< 90^0\) (phải giả sử nhé).
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=2\Rightarrow\sin\alpha=2.\cos\alpha\)
\(\sin\alpha^2+\cos\alpha^2=1\)
\(\Rightarrow4\cos\alpha^2+\cos\alpha^2=1\)
\(\Rightarrow5\cos\alpha^2=1\)
\(\Rightarrow\cos\alpha^2=\dfrac{1}{5}\)
\(\Rightarrow\cos\alpha=\dfrac{\sqrt{5}}{5}\).
\(\sin\alpha=2\cos\alpha=2.\dfrac{\sqrt{5}}{5}=\dfrac{2\sqrt{5}}{5}\).
\(\cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{2}\)
Bài 13:
\(\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\cos^220^0+\cos^240^0+\sin^2\left(90^0-50^0\right)+\sin^2\left(90^0-70^0\right)\)
\(=\cos^220^0+\cos^240^0+\sin^240^0+\sin^220^0\)
\(=\left(\sin^220^0+\cos20^0\right)+\left(\sin^240^0+\cos40^0\right)\)
\(=1+1=2\)

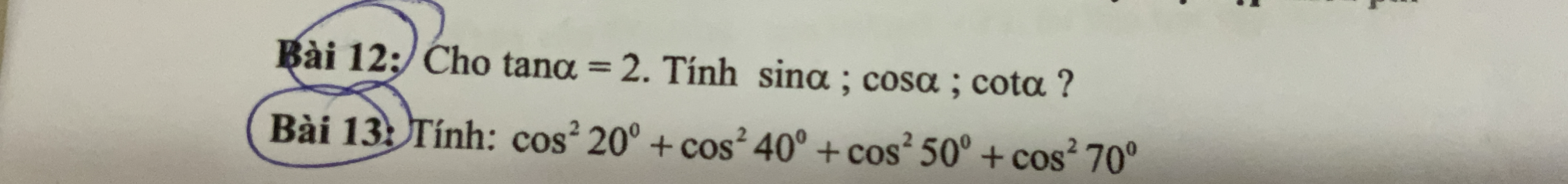 giúp mik vs
giúp mik vs