\(\dfrac{x}{x^2-x+1}=\dfrac{2}{3}\\ \Rightarrow2x^2-2x+2=3x\\ \Rightarrow2x^2-5x+2=0\\ \Rightarrow\left(2x^2-4x\right)-\left(x-2\right)=0\\ \Rightarrow2x\left(x-2\right)-\left(x-2\right)=0\\ \Rightarrow\left(x-2\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2}\end{matrix}\right.\)
Thay x=2 vào Q ta có:
\(Q=\dfrac{x^2}{x^4+x^2+1}=\dfrac{2^2}{2^4+2^2+1}=\dfrac{4}{21}\)
Thay x=\(\dfrac{1}{2}\) vào Q ta có:
\(Q=\dfrac{x^2}{x^4+x^2+1}=\dfrac{\left(\dfrac{1}{2}\right)^2}{\left(\dfrac{1}{2}\right)^4+\left(\dfrac{1}{2}\right)^2+1}=\dfrac{4}{21}\)






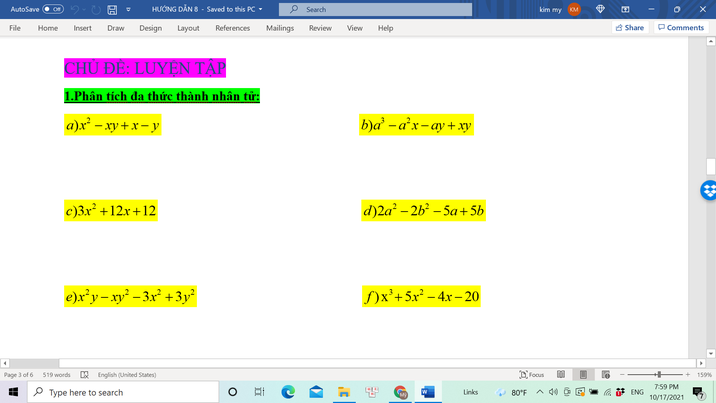


 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều





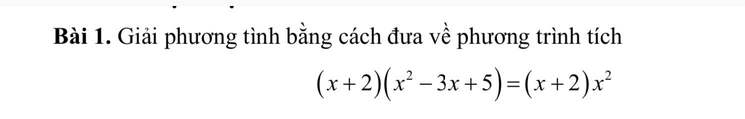



 giúp mik vs mik đag cần gấp
giúp mik vs mik đag cần gấp