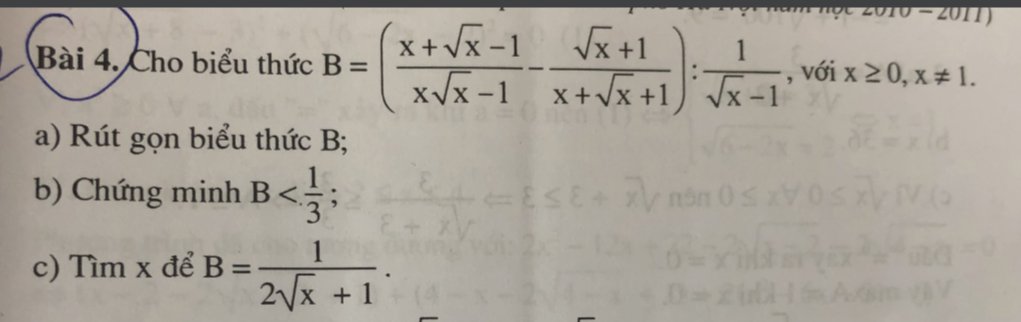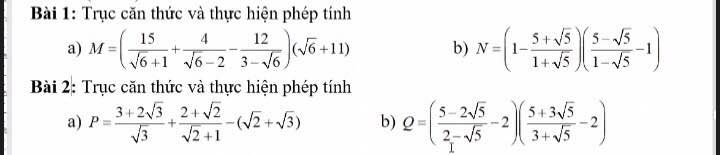a. \(BC=BH+HC=5\left(cm\right)\)
\(\left\{{}\begin{matrix}AH=\sqrt{BH\cdot HC}=2,4\left(cm\right)\\AC=\sqrt{CH\cdot BC}=4\left(cm\right)\\AB=\sqrt{BH\cdot BC}=3\left(cm\right)\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{B}\approx53^0\\\widehat{C}=90^0-\widehat{B}\approx37^0\end{matrix}\right.\)
c. Áp dụng HTL: \(\left\{{}\begin{matrix}BK\cdot BD=AB^2\\BH\cdot BC=AB^2\end{matrix}\right.\Rightarrow BH\cdot BC=BK\cdot BD\)
Đúng 0
Bình luận (0)
