\(\int_{-1}^1\sqrt{e^{2x}-2e^x+1}dx\)
\(=\int_{-1}^1\left|e^x-1\right|dx\)
\(=\int_{-1}^0\left(1-e^x\right)dx+\int_0^1\left(e^x-1\right)dx\)
\(=\left(x-e^x\right)|^0_{-1}+\left(e^x-x\right)|^1_0\)
\(=\left(\dfrac{1}{e}\right)+\left(e-2\right).\)
\(=\left(\sqrt{e}-\dfrac{1}{\sqrt{e}}\right)^2\)

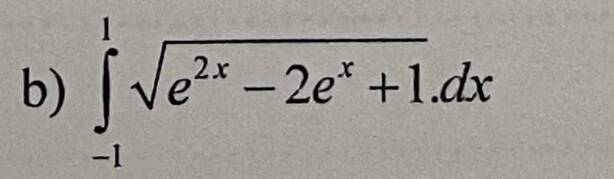



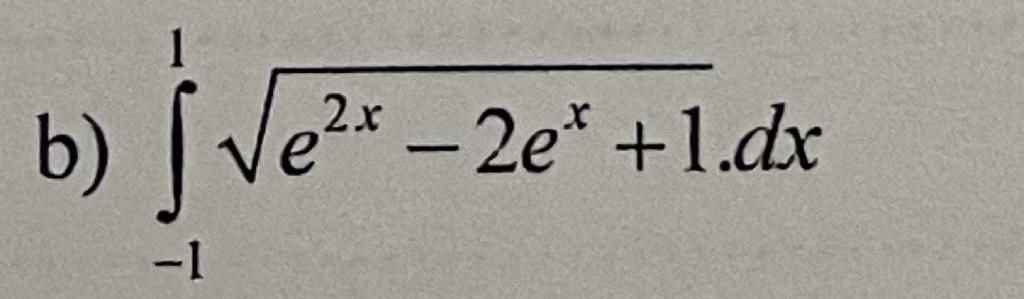 giúp mik với
giúp mik với







 Giải giúp mik câu 27 và 28 với
Giải giúp mik câu 27 và 28 với