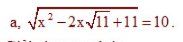c: \(A=\dfrac{\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+4+\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
Để \(A< \dfrac{2}{3}\) thì \(A-\dfrac{2}{3}< 0\)
=>\(\dfrac{\sqrt{x}+1}{\sqrt{x}+2}-\dfrac{2}{3}< 0\)
=>\(\dfrac{3\left(\sqrt{x}+1\right)-2\left(\sqrt{x}+2\right)}{3\left(\sqrt{x}+2\right)}< 0\)
=>\(3\left(\sqrt{x}+1\right)-2\left(\sqrt{x}+2\right)< 0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<x<1

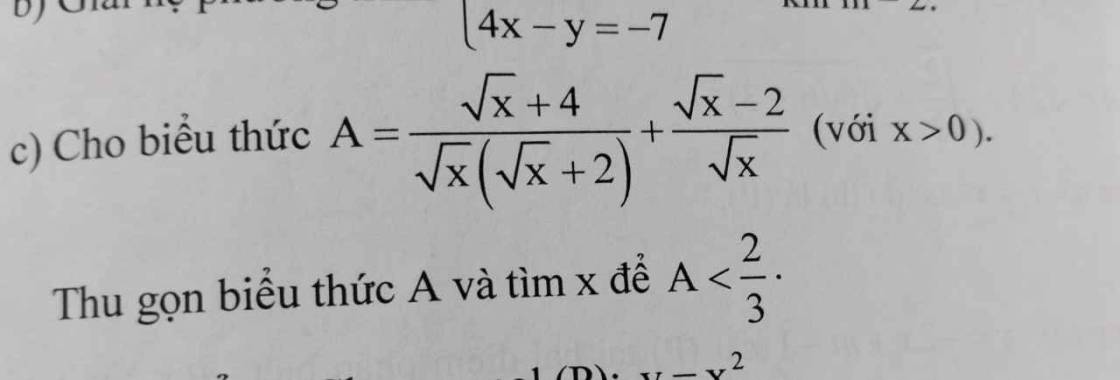




 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 
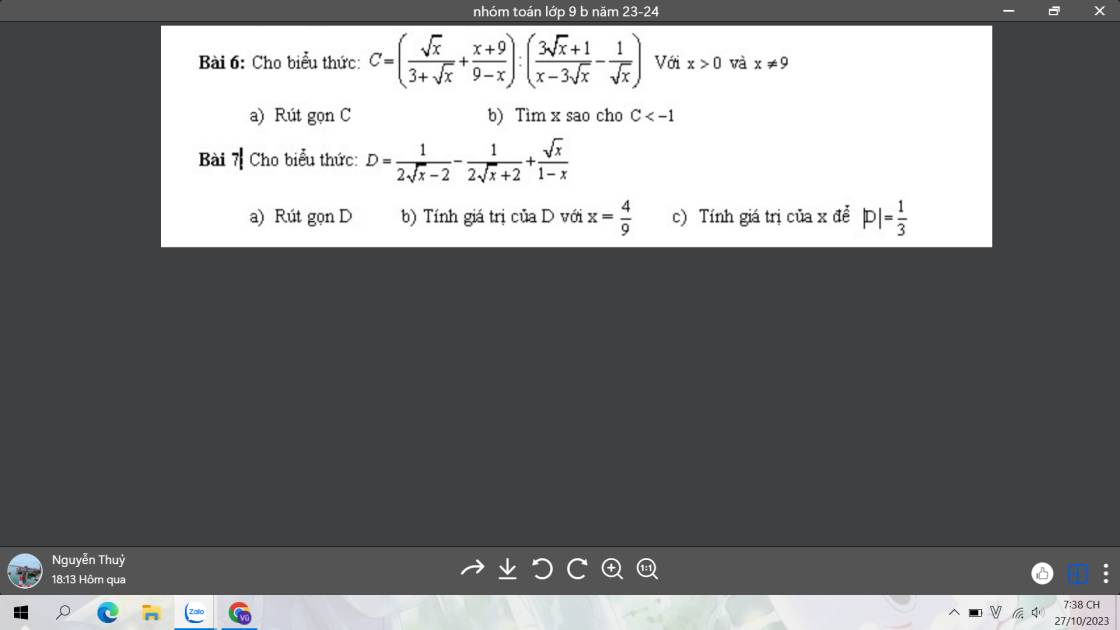 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp



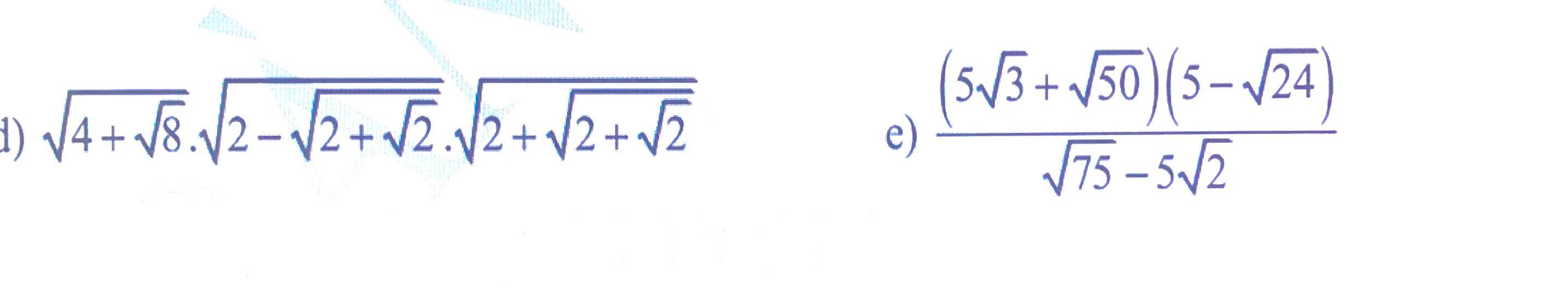


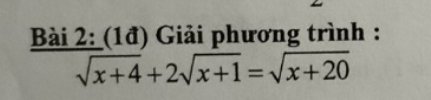
 giúp mik với mn ơi
giúp mik với mn ơi