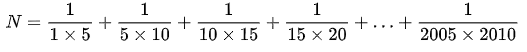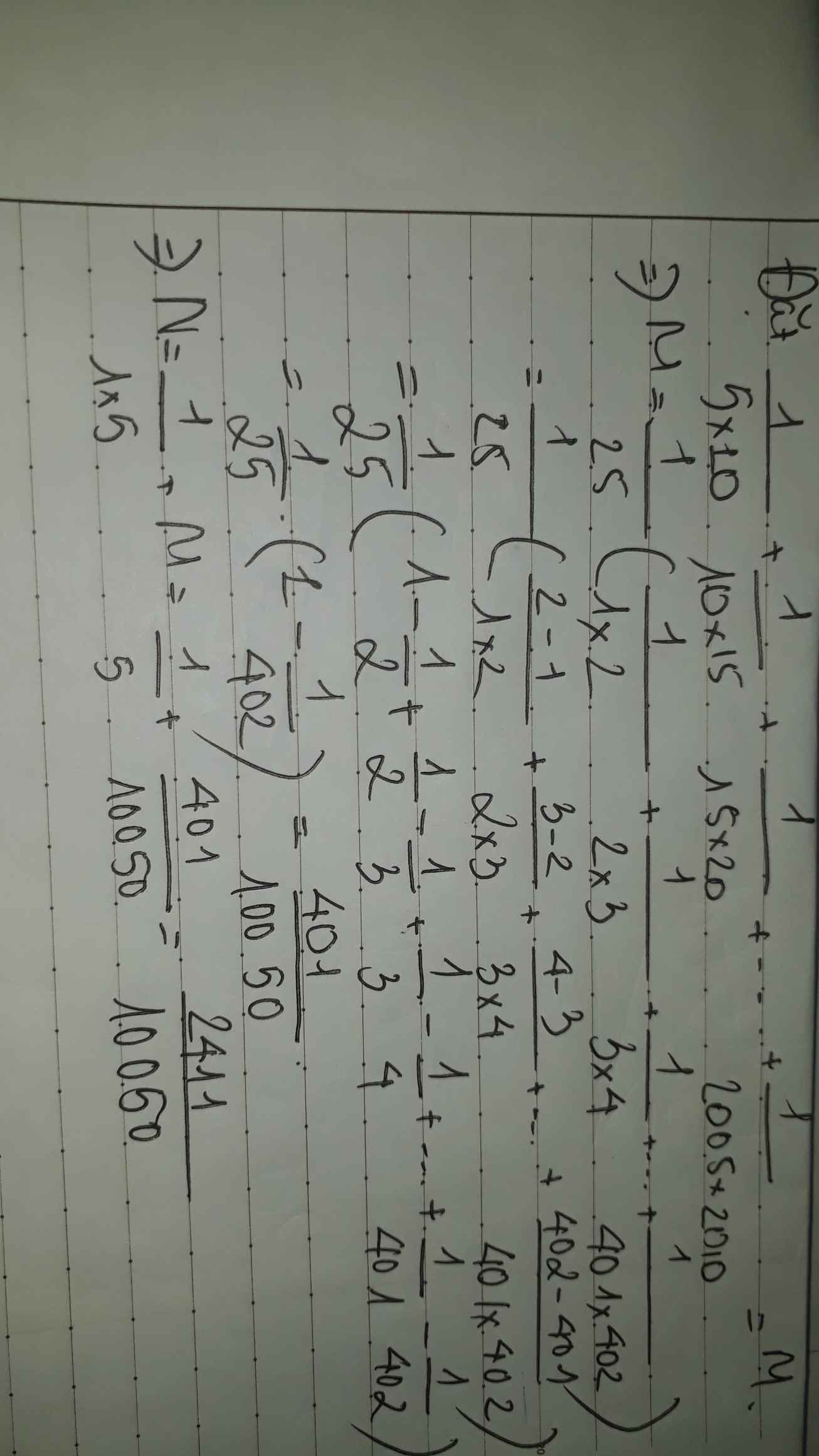\(N=\) \(\dfrac{1}{1\times5}+\dfrac{1}{5\times10}+\dfrac{1}{10\times15}+\dfrac{1}{15\times20}+...+\dfrac{1}{2005\times2010}\)
\(N=\) \(\dfrac{1}{1\times5}+\dfrac{1}{5}\times\left(\dfrac{5}{5\times10}+\dfrac{5}{10\times15}+\dfrac{5}{15\times20}+...+\dfrac{5}{2005\times2010}\right)\)
\(N=\) \(\dfrac{1}{5}+\dfrac{1}{5}\times\left(\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{0}-\dfrac{1}{15}+...\dfrac{1}{2005}-\dfrac{1}{2010}\right)\)
\(N=\) \(\dfrac{1}{5}+\dfrac{1}{5}\times\left(\dfrac{1}{5}-\dfrac{1}{2010}\right)\)
\(N=\) \(\dfrac{1}{5}\times\left(1+\dfrac{1}{5}-\dfrac{1}{2010}\right)\)
\(N=\) \(\dfrac{1}{5}\times\dfrac{2411}{2010}\)
\(N=\) \(\dfrac{2411}{10050}\)
Ta có: \(N=\dfrac{1}{1\cdot5}+\dfrac{1}{5\cdot10}+\dfrac{1}{10\cdot15}+...+\dfrac{1}{2005\cdot2010}\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\left(\dfrac{5}{5\cdot10}+\dfrac{5}{10\cdot15}+...+\dfrac{5}{2005\cdot2010}\right)\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\left(\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{15}+...+\dfrac{1}{2005}-\dfrac{1}{2010}\right)\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\left(\dfrac{1}{5}-\dfrac{1}{2010}\right)\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\cdot\dfrac{401}{2010}\)
\(=\dfrac{1}{5}\cdot\dfrac{2411}{2010}=\dfrac{2411}{10050}\)