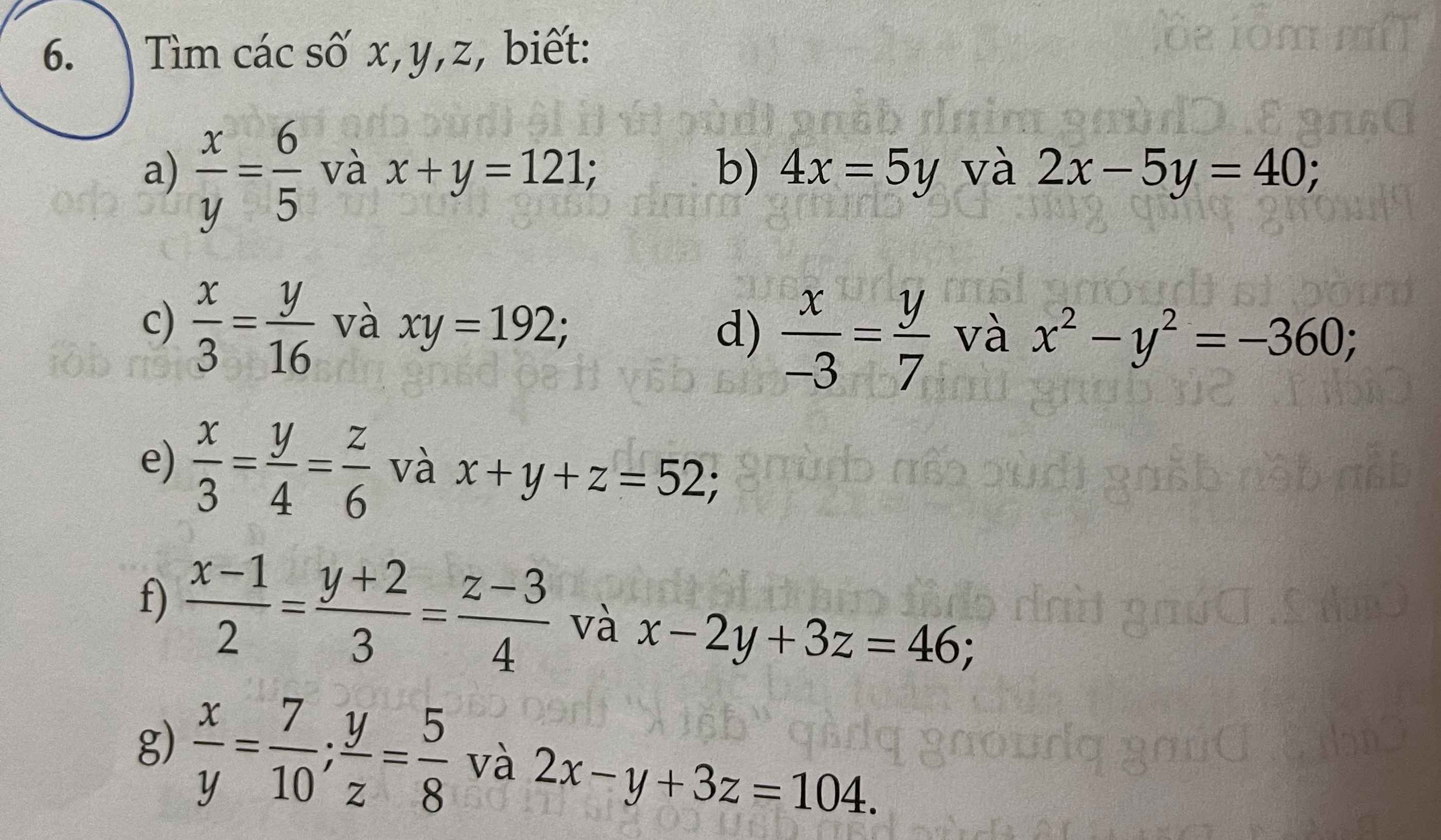\(\dfrac{x}{y}=\dfrac{6}{5}\)⇒\(\dfrac{x}{6}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+y}{6+5}=\dfrac{121}{11}=11\)
⇒\(x=66;y=55\)
các bạn giải rõ giúp mik nha! rùi mik tik cho, :3
b: Ta có: 4x=5y
nên \(\dfrac{x}{5}=\dfrac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{2x-5y}{2\cdot5-5\cdot4}=\dfrac{40}{-10}=-4\)
Do đó: x=-20; y=-16
a. Theo đề ta có: 5x = 6y
Ta có HPT: \(\left\{{}\begin{matrix}x+y=121\\5x=6y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=121\\5x-6y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+5y=605\\5x-6y=0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}11y=605\\5x-6y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=55\\x=66\end{matrix}\right.\)
Các câu còn lại tương tự
\(a,\dfrac{x}{y}=\dfrac{6}{5}\Rightarrow\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+y}{6+5}=\dfrac{121}{11}=11\\ \Rightarrow\left\{{}\begin{matrix}x=66\\y=55\end{matrix}\right.\\ b,4x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{2x-5y}{10-20}=\dfrac{40}{-10}=-4\\ \Rightarrow\left\{{}\begin{matrix}x=-20\\y=-16\end{matrix}\right.\\ c,\dfrac{x}{3}=\dfrac{y}{16}=k\Rightarrow x=3k;y=16k\\ xy=192\Rightarrow3k\cdot16k=192\Rightarrow48k^2=192\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6;y=32\\x=-6;y=-32\end{matrix}\right.\)
\(d,\dfrac{x}{-3}=\dfrac{y}{7}=k\Rightarrow x=-3k;y=7k\\ x^2-y^2=-360\Rightarrow9k^2-49k^2=-360\Rightarrow-40k^2=-360\Rightarrow k^2=9\\ \Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-9;y=21\\x=9;y=-21\end{matrix}\right.\)
\(e,\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{6}=\dfrac{x+y+z}{3+4+6}=\dfrac{52}{13}=4\\ \Rightarrow\left\{{}\begin{matrix}x=12\\y=16\\z=24\end{matrix}\right.\\ f,\dfrac{x-1}{2}=\dfrac{y+2}{3}=\dfrac{z-3}{4}=k\Rightarrow x=2k+1;y=3k-2;z=4k+3\\ x-2y+3z=46\Rightarrow2k+1-2\left(3k-2\right)+3\left(4k+3\right)=46\\ \Rightarrow2k+1-6k+4+12k+9=46\\ \Rightarrow8k=32\Rightarrow k=4\Rightarrow\left\{{}\begin{matrix}x=9\\y=10\\z=19\end{matrix}\right.\)