a: \(\left|2x-27\right|^{2007}+\left(3y+10\right)^{2008}\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(\dfrac{27}{2};-\dfrac{10}{3}\right)\)
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{x-1-2y+4+3z-9}{2-2\cdot3+3\cdot4}=\dfrac{-10-6}{8}=-2\)
Do đó: \(\left\{{}\begin{matrix}x-1=-4\\y-2=-6\\z-3=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-4\\z=-5\end{matrix}\right.\)

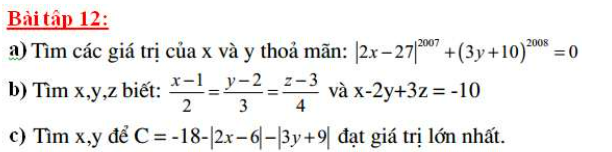











 mn giúp mik vs mik cần gấp( có trình bày nha~)
mn giúp mik vs mik cần gấp( có trình bày nha~)